题目内容
14.某商家销售一种成本为每件50元的商品.据市场调查分析,如果按每件60元销售,一周能售出400件;若销售单价每涨1元,每周销售量就减少8件.设销售单价为x元(x≥60),一周的销售量为y件.(1)求y与x之间的函数表达式,并写出自变量x的取值范围;
(2)设一周的销售利润为W元,求W关于x的函数表达式,并求出商家销售该商品的最大利润;
(3)若该商家每周投入此商品的成本不超过10000元,问销售单价定位多少时,销售该商品一周的利润能达到6400元.
分析 (1)根据题意可得销量=400-8(销售单价-60),进而得出函数关系式;
(2)用配方法化简解析式,可得y=-8(x-80)2+7200,当60≤x<80时,利润随着单价的增大而增大进而得出答案.
(3)令y=6400,求出x的实际取值,结合此商品的成本不超过10000元得出答案.
解答 解:(1)由题意得:
y=400-8(x-60)=880-8x(60≤x≤110);
(2)根据题意可得:W=(x-50)(880-8x)
=-8x2+1280x-44000
=-8(x-80)2+7200
当60≤x<80时,利润随着单价的增大而增大,即最大利润为7200元;
(3)由题意得:-8(x-80)2+7200=6400
解得:x1=70,x2=90,
当x=70时,成本=50×(880-8x)=16000>10000不符合要求,舍去.
当x=90时,成本=50×(880-8x)=8000<10000符合要求.
答:销售单价应定为90元,才能使得一周销售利润达到6400元的同时,投入不超过10000元.
点评 此题主要考查了二次函数的应用以及用配方法求出最大值,准确分析题意,列出y与x之间的二次函数关系式是解题关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
5.(1)如图1,AB=AD,∠B=∠D,∠1=∠2,求证:△ABC≌△ADE.
(2)如图2,已知,AD是△ABC的BC边上的中线,点E,F分别是AD及其延长线上的点,且DE=DF,求证:BF∥CE.

(2)如图2,已知,AD是△ABC的BC边上的中线,点E,F分别是AD及其延长线上的点,且DE=DF,求证:BF∥CE.

4. 如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
 如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )| A. | (0,1) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | ($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) |
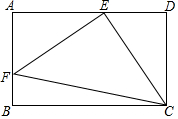 如图,在矩形ABCD中,E为AD上的一点,F为AB上的点,且DE=AF,EF=EC,连结FC.
如图,在矩形ABCD中,E为AD上的一点,F为AB上的点,且DE=AF,EF=EC,连结FC. 已知:如图,AP=DP,∠A=∠D.
已知:如图,AP=DP,∠A=∠D.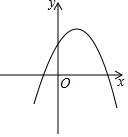 二次函数y=ax2-3ax+2(a<0)的图象如图所示,若y<2,则x的取值范围为x<0或x>3.
二次函数y=ax2-3ax+2(a<0)的图象如图所示,若y<2,则x的取值范围为x<0或x>3.