题目内容
13.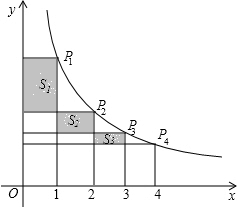 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )| A. | $\frac{5}{12}$k | B. | $\frac{1}{2}$k | C. | $\frac{7}{12}$k | D. | $\frac{2}{3}$k |
分析 先根据题意求出点P1、P2、P3、P4的坐标,再利用矩形的面积公式列式解答即可.
解答 解:∵反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,
∴P1(1,k),P2(2,$\frac{k}{2}$)P3(3,$\frac{k}{3}$),P4(4,$\frac{k}{4}$),
∴S1+S3-S2=1•k+1•($\frac{k}{3}$-$\frac{k}{4}$)-1•($\frac{k}{2}$-$\frac{k}{3}$)
=k+$\frac{k}{12}$-$\frac{k}{6}$
=$\frac{5}{12}$k.
故选A.
点评 本题考查的是反比例函数图象上点的坐标特征,矩形的面积公式,根据题意得出P1、P2、P3、P4的坐标是解答此题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
3.有m个数的平均数是x,n个数的平均数为y,则这(m+n)个数的平均数为( )
| A. | $\frac{x+y}{m+n}$ | B. | $\frac{mx+ny}{m+n}$ | C. | $\frac{mx+ny}{x+y}$ | D. | $\frac{mx+ny}{2}$ |
18.如果a是任意实数,下列各式中一定有意义的是( )
| A. | $\sqrt{a}$ | B. | $\sqrt{\frac{1}{{a}^{2}}}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{-{a}^{2}}$ |
5.为了了解学生作文考试“书写分”得分情况,李老师随机抽取了10位学生的得分,如图1所示:
(1)利用图1中的信息,补全下表:
(2)李老师把图1转化成图2所示的条形图,请你帮李老师补全条形图;
(3)李老师的学生有60位,请你帮李老师估计得4分以上(含4分)的学生有多少位?
(1)利用图1中的信息,补全下表:
| 平均数(分) | 中位数(分) | 众数(分) |
| 3.4 | 4 | 4 |
(3)李老师的学生有60位,请你帮李老师估计得4分以上(含4分)的学生有多少位?

3.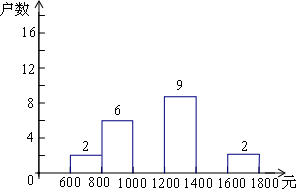 小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
根据以上提供的信息,解答下列问题:
(1)频数分布表中:a=16,b=5,c=12.5%.
(2)补全频数分布直方图.
(3)请估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
 小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
小明在学校组织的社会调查活动中负责了解他所居住的小区560户居民的家庭收入情况.他从中随机调查了一定户数的家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.| 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | a | 40% |
| 1200≤x<1400 | 9 | 22.5% |
| 1400≤x<1600 | b | c |
| 1600≤x<1800 | 2 | 5% |
| 合计 | 40 | 100% |
(1)频数分布表中:a=16,b=5,c=12.5%.
(2)补全频数分布直方图.
(3)请估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
 某工厂车间共有10名工人,调查每个工人的日均生产能力,获得数据制成如下统计图.
某工厂车间共有10名工人,调查每个工人的日均生产能力,获得数据制成如下统计图.