题目内容
8.(1)因式分解:(x-8)(x+2)+6x(2)解不等式组$\left\{\begin{array}{l}{5x-2>3(x+1)}\\{\frac{1}{2}x-3≤5-\frac{3}{2}x}\end{array}\right.$,并写出它的整数解.
分析 (1)去括号、合并同类项后根据平方差公式分解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原式=x2-6x-16+6x
=x2-16
=(x+4)(x-4);
(2)解不等式5x-2>3(x+1),得:x>$\frac{5}{2}$,
解不等式$\frac{1}{2}$x-3≤5-$\frac{3}{2}$x,得:x≤4,
则不等式组的解集为$\frac{5}{2}$<x≤4,
∴其整数解为3、4.
点评 本题考查的是因式分解和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
13.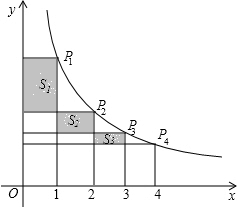 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )| A. | $\frac{5}{12}$k | B. | $\frac{1}{2}$k | C. | $\frac{7}{12}$k | D. | $\frac{2}{3}$k |
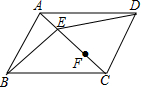 如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).
如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).