题目内容
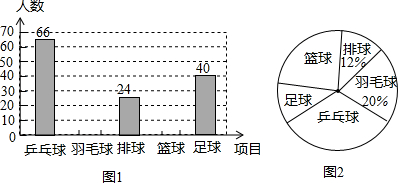
2. 某工厂车间共有10名工人,调查每个工人的日均生产能力,获得数据制成如下统计图.
某工厂车间共有10名工人,调查每个工人的日均生产能力,获得数据制成如下统计图.(1)求这10名工人的日均生产件数的平均数、众数、中位数;
(2)若要使占60%的工人都能完成任务,应选什么统计量(平均数、中位数、众数)做日生产件数的定额?
分析 (1)根据平均数=加工零件总数÷总人数,中位数是将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数,如果数据的个数是偶数就是中间两个数的平均数,众数是指一组数据中出现次数最多的数据,分别进行解答即可得出答案.
(2)应根据平均数、中位数和众数和本题的60%可知选择哪个统计量比较合适.
解答 解:(1)由统计图可得,
平均数为:(8×3+10+12×2+13×4)÷10=11(件),
∵13出现了4次,出现的次数最多,
∴众数是13;
把这些数从小到大排列为:8,8,8,10,12,12,13,13,13,13,最中间的数是第5、6个数的平均数,则中位数是$\frac{12+12}{2}$=12;
(2)由题意可得,若要使占60%的工人都能完成任务,应选中位数作为日生产件数的定额.
点评 本题考查统计量的选择、平均数、中位数和众数,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.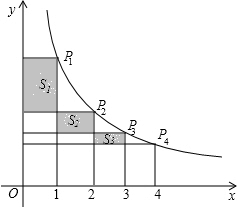 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )| A. | $\frac{5}{12}$k | B. | $\frac{1}{2}$k | C. | $\frac{7}{12}$k | D. | $\frac{2}{3}$k |