题目内容
1.计算:(1)$\sqrt{18}$-$\sqrt{32}$+$\sqrt{\frac{1}{2}}$;
(2)(2$\sqrt{2}$+3$\sqrt{3}$)2.
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)利用完全平方公式计算.
解答 解:(1)原式=3$\sqrt{2}$-4$\sqrt{2}$+$\frac{\sqrt{2}}{2}$
=-$\frac{\sqrt{2}}{2}$;
(2)原式=8+12$\sqrt{6}$+27
=35+12$\sqrt{6}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
9.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=5k}\\{x-y=9k}\end{array}\right.$的解也是2x+3y<16的解,则( )
| A. | k<0 | B. | k<-1 | C. | k<2 | D. | k<1 |
13.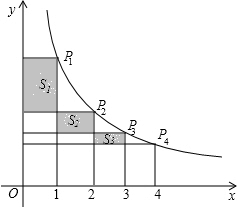 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象上有四个点P1,P2,P3,P4,它们的横坐标分别为1,2,3,4,分别向x轴,y轴作垂线,图中所构成的阴影部分面积分别为S1,S2,S3,则S1+S3-S2的值为( )| A. | $\frac{5}{12}$k | B. | $\frac{1}{2}$k | C. | $\frac{7}{12}$k | D. | $\frac{2}{3}$k |
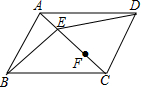 如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).
如图,E、F是?ABCD的对角线AC上的两点,且AE=CF,请你以点F为一个端点与图中已标明字母的某一点连成一条线段,猜想并说明它与图中已有的某一条线段相等(只需说明一组线段相等即可).