��Ŀ����
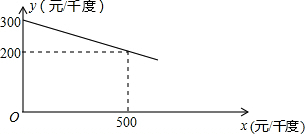
��֪����ͼ��O1Ϊx����һ�㣬��O1ΪԲ������O1��x����C��D���㣬��y����M��N���㣬��CMD�����ƽ���߽���O1�ڵ�E��AB���ң���AB��CD��ֱ��DM�Ľ���ʽΪy=3x+3��
��1����ͼ1�����O1�뾶����E�����꣮
��2����ͼ2����E��EF��BC��F����A��BΪ��CND������������AB��CD�����ʣ�BF+CF��AC֮���Ƿ����ij�ֵ�����ϵ����д����Ľ��ۣ���֤����
��3���ڣ�2���������£�EF����O1�ڵ�G������BG�ij����Ƿ�仯��������ֱ��д��BG�ij�����д���̣������仯�Ի�ͼ˵�����ɣ�

��1����ͼ1�����O1�뾶����E�����꣮
��2����ͼ2����E��EF��BC��F����A��BΪ��CND������������AB��CD�����ʣ�BF+CF��AC֮���Ƿ����ij�ֵ�����ϵ����д����Ľ��ۣ���֤����
��3���ڣ�2���������£�EF����O1�ڵ�G������BG�ij����Ƿ�仯��������ֱ��д��BG�ij�����д���̣������仯�Ի�ͼ˵�����ɣ�

���㣺Բ���ۺ���,ȫ�������ε��ж�������,���ɶ���,��������λ�߶���,���ε��ж�������,��������,Բ�Ľǡ������ҵĹ�ϵ,Բ�ܽǶ���,Բ�ڽ��ı��ε�����
ר�⣺ѹ����
��������1������ED��EC��EO1��MO1����ͼ1������֤����ECD=��SME=��EMC=��EDC���Ӷ�����֤����EO1D=��EO1C=90�㣮��ֱ��DM�Ľ���ʽΪy=3x+3�ɵ�OD=1��OM=3�����O1�İ뾶Ϊr����Rt��MOO1�����ù��ɶ����Ϳɽ�����⣮
��2������O1��O1P��EG��P������O1��O1Q��BC��Q������EO1��DB����ͼ2����AB��DC��֤��BD=AC����֤�ı���O1PFQ�Ǿ��Σ��Ӷ���O1P=FQ����PO1Q=90�㣬�����С�EO1P=��CO1Q���Ӷ�����֤����EPO1�ա�CQO1������PO1=QO1��������������λ�߶����ɵ�FQ=
BD���Ӷ����Եõ�BF+CF=2FQ=AC��
��3������EO1��ED��EB��BG����ͼ3����֤EF��BD�����С�GEB=��EBD���Ӷ���
=
��Ҳ����BG=DE����Rt��EO1D�����ù��ɶ������ED���Ϳɽ�����⣮
��2������O1��O1P��EG��P������O1��O1Q��BC��Q������EO1��DB����ͼ2����AB��DC��֤��BD=AC����֤�ı���O1PFQ�Ǿ��Σ��Ӷ���O1P=FQ����PO1Q=90�㣬�����С�EO1P=��CO1Q���Ӷ�����֤����EPO1�ա�CQO1������PO1=QO1��������������λ�߶����ɵ�FQ=
| 1 |
| 2 |
��3������EO1��ED��EB��BG����ͼ3����֤EF��BD�����С�GEB=��EBD���Ӷ���
 |
| BG |
 |
| ED |
����⣺��1������ED��EC��EO1��MO1����ͼ1��
��MEƽ�֡�SMC��
���SME=��EMC��
�ߡ�SME=��ECD����EMC=��EDC��
���ECD=��EDC��
���EO1D=��EO1C��
�ߡ�EO1D+��EO1C=180�㣬
���EO1D=��EO1C=90�㣮
��ֱ��DM�Ľ���ʽΪy=3x+3��
���M��������0��3������D��������-1��0����
��OD=1��OM=3��
���O1�İ뾶Ϊr����MO1=DO1=r��
��Rt��MOO1��
��r-1��2+32=r2��
��ã�r=5��
��OO1=4��EO1=5��
���O1�뾶Ϊ5����E������Ϊ��4��5����
��2��BF+CF=AC��
֤��������O1��O1P��EG��P������O1��O1Q��BC��Q������EO1��DB����ͼ2��
��AB��DC�����DCA=��BAC��
��
=
��
��
=
��
��BD=AC��
��O1P��EG��O1Q��BC��EF��BF��
���O1PF=��PFQ=��O1QF=90�㣮
���ı���O1PFQ�Ǿ��Σ�
��O1P=FQ����PO1Q=90�㣮
���EO1P=90��-��PO1C=��CO1Q��
�ڡ�EPO1�͡�CQO1�У�
��
���EPO1�ա�CQO1��
��PO1=QO1��
��FQ=QO1��
��QO1��BC����BQ=CQ��
��CO1=DO1����O1Q=
BD��
��FQ=
BD��
��BF+CF=FQ+BQ+CF=FQ+CQ+CF=2FQ��
��BF+CF=BD=AC��
��3������EO1��ED��EB��BG����ͼ3��
��DC�ǡ�O1��ֱ�������DBC=90�㣮
���DBC+��EFB=180�㣮
��EF��BD��
���GEB=��EBD��
��
=
��
��BG=DE��
��DO1=EO1=5��EO1��DO1��
��DE=5
��
��BG=5
��
����BG�ij��Ȳ��䣬����5
��
��MEƽ�֡�SMC��

���SME=��EMC��
�ߡ�SME=��ECD����EMC=��EDC��
���ECD=��EDC��
���EO1D=��EO1C��
�ߡ�EO1D+��EO1C=180�㣬
���EO1D=��EO1C=90�㣮
��ֱ��DM�Ľ���ʽΪy=3x+3��
���M��������0��3������D��������-1��0����
��OD=1��OM=3��
���O1�İ뾶Ϊr����MO1=DO1=r��
��Rt��MOO1��
��r-1��2+32=r2��
��ã�r=5��
��OO1=4��EO1=5��
���O1�뾶Ϊ5����E������Ϊ��4��5����
��2��BF+CF=AC��
֤��������O1��O1P��EG��P������O1��O1Q��BC��Q������EO1��DB����ͼ2��
��AB��DC�����DCA=��BAC��
��
 |
| AD |
 |
| BC |
��
 |
| BD |
 |
| AC |
��BD=AC��
��O1P��EG��O1Q��BC��EF��BF��
���O1PF=��PFQ=��O1QF=90�㣮
���ı���O1PFQ�Ǿ��Σ�
��O1P=FQ����PO1Q=90�㣮

���EO1P=90��-��PO1C=��CO1Q��
�ڡ�EPO1�͡�CQO1�У�
|
���EPO1�ա�CQO1��
��PO1=QO1��
��FQ=QO1��
��QO1��BC����BQ=CQ��
��CO1=DO1����O1Q=
| 1 |
| 2 |
��FQ=
| 1 |
| 2 |
��BF+CF=FQ+BQ+CF=FQ+CQ+CF=2FQ��
��BF+CF=BD=AC��
��3������EO1��ED��EB��BG����ͼ3��

��DC�ǡ�O1��ֱ�������DBC=90�㣮
���DBC+��EFB=180�㣮
��EF��BD��
���GEB=��EBD��
��
 |
| BG |
 |
| ED |
��BG=DE��
��DO1=EO1=5��EO1��DO1��
��DE=5
| 2 |
��BG=5
| 2 |
����BG�ij��Ȳ��䣬����5
| 2 |
���������⿼����Բ�ܽǶ�����Բ�ڽ��ı��ε����ʡ������ҵĹ�ϵ������������ȫ�������ε��ж������ʡ����ε��ж������ʡ���������λ�߶�����ƽ���ߵ��ж������ʡ����ɶ�����֪ʶ���ۺ��ԱȽ�ǿ����һ�����Ѷȣ�����AB��DC֤��AC=BD�ǽ���ڣ�2��С��Ĺؼ�����EG��DB֤��BG=DE�ǽ���ڣ�3��С��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
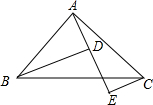 ��ͼ��ʾ��A��D��E������ͬһֱ���ϣ��ҡ�BAD�ա�ACE��
��ͼ��ʾ��A��D��E������ͬһֱ���ϣ��ҡ�BAD�ա�ACE�� ��ͼ��C���߶�AB���е㣬��1=��2=��3��CD=CE��
��ͼ��C���߶�AB���е㣬��1=��2=��3��CD=CE�� ��ͼ���ڡ�ABC�У�D��E��F���ֱ���AB��BC��AC���е㣬��֤���ı���BEFD��ƽ���ı��Σ�
��ͼ���ڡ�ABC�У�D��E��F���ֱ���AB��BC��AC���е㣬��֤���ı���BEFD��ƽ���ı��Σ�