题目内容
 如图,C是线段AB的中点,∠1=∠2=∠3,CD=CE.
如图,C是线段AB的中点,∠1=∠2=∠3,CD=CE.(1)求证:△ACD≌△BCE.
(2)若∠D=50°,求∠B的度数.
考点:全等三角形的判定与性质
专题:
分析:(1)利用中点性质可得AC=BC,在利用SAS定理证明△ACD≌△BCE.
(2)根据平角定义计算出∠1的度数,再根据三角形内角和定理可得∠A的度数,然后根据全等三角形对应角相等可得∠B的度数.
(2)根据平角定义计算出∠1的度数,再根据三角形内角和定理可得∠A的度数,然后根据全等三角形对应角相等可得∠B的度数.
解答:证明:(1)∵C是线段AB的中点,
∴AC=BC,
在△ADC和△EBC中,
,
∴△ACD≌△BCE(SAS);
(2)∵∠1=∠2=∠3,
∴∠1=60°,
∵∠D=50°,
∴∠A=180°-50°-60°=70°,
∵△ACD≌△BCE,
∴∠B=∠A=70°.
∴AC=BC,
在△ADC和△EBC中,
|
∴△ACD≌△BCE(SAS);
(2)∵∠1=∠2=∠3,
∴∠1=60°,
∵∠D=50°,
∴∠A=180°-50°-60°=70°,
∵△ACD≌△BCE,
∴∠B=∠A=70°.
点评:此题主要考查了全等三角形的判定与性质,关键是掌握证明三角形全等的判定方法:SSS、ASA、SAS、AAS、HL.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
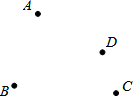 点A,B,C,D的位置如图,按下列要求画出图形.
点A,B,C,D的位置如图,按下列要求画出图形.



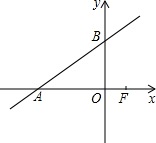 如图,已知直线y=
如图,已知直线y=