题目内容
己知函数y=(k-3)x8-k2为反比例函数.
(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 ;(填变化情况)
(3)当-2≤x≤-
时,此函数的最大值为 ,最小值为 .
(1)求k的值;
(2)它的图象在第
(3)当-2≤x≤-
| 1 |
| 2 |
考点:反比例函数的性质,反比例函数的定义
专题:
分析:(1)首先根据反比例函数的定义可得8-k2=-1,且k-3≠0,解出k的值即可;
(2)根据k<0,结合反比例函数的性质可得答案;
(3)根据y随x增大而增大可得当x=-2时,y最小,当x=-
时,y最大,代入求值即可.
(2)根据k<0,结合反比例函数的性质可得答案;
(3)根据y随x增大而增大可得当x=-2时,y最小,当x=-
| 1 |
| 2 |
解答:解:(1)由题意得:8-k2=-1,且k-3≠0,
解得:k=-3,;
(2)∵k=-3<0,
∴图象在第二、四象限,在各象限内,y随x增大而增大;
故答案为:二、四;增大;
(3)当x=-2时,y最小=
=3;
当x=-
时,y最大=
=12;
故答案为:12;3.
解得:k=-3,;
(2)∵k=-3<0,
∴图象在第二、四象限,在各象限内,y随x增大而增大;
故答案为:二、四;增大;
(3)当x=-2时,y最小=
| -6 |
| -2 |
当x=-
| 1 |
| 2 |
| -6 | ||
-
|
故答案为:12;3.
点评:此题主要考查了反比例函数的性质和定义,关键是掌握反比例函数的形式为y=
(k为常数,k≠0)或y=kx-1(k为常数,k≠0).
| k |
| x |

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
下列命题的逆命题成立的是( )
| A、对顶角相等 |
| B、如果两个实数相等,那么它们的绝对值相等 |
| C、全等三角形的对应角相等 |
| D、两条直线平行,内错角相等 |
下列各组式子中是同类项的是( )
| A、-2a与a2 |
| B、5ab2c与-b2ac |
| C、2a2b与3ab2 |
| D、-17ab2和4ab2c |
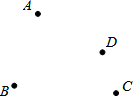 点A,B,C,D的位置如图,按下列要求画出图形.
点A,B,C,D的位置如图,按下列要求画出图形. 如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F. 如图,⊙O是△ABC的外接圆,AF平分∠BAC交BC于点E,交⊙O于点F,BD平分∠ABC交AF于点D,过点F作FH∥BC.
如图,⊙O是△ABC的外接圆,AF平分∠BAC交BC于点E,交⊙O于点F,BD平分∠ABC交AF于点D,过点F作FH∥BC.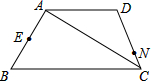 如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AB中点,请在对角线AC上找一点M使EM+MN的值最小,并求出EM+MN的最小值.
如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AB中点,请在对角线AC上找一点M使EM+MN的值最小,并求出EM+MN的最小值.