题目内容

如图，在△ABC中，D，E，F，分别是AB，BC，AC的中点，求证：四边形BEFD是平行四边形．
考点：平行四边形的判定,三角形中位线定理
专题：证明题
分析：利用三角形中位线定理判定四边形BEFD的两组对边相互平行，则四边形BEFD是平行四边形．
解答：证明：如图，∵D，F分别是AB，AC的中点，
∴DF∥BC，则DF∥BE．
又∵E，F分别是BC，AC的中点，
∴EF∥AB，则EF∥DB，
∴四边形BEFD是平行四边形．
点评：本题主要考查了三角形的中位线定理，勾股定理以及平行四边形的判定定理，关键是掌握三角形中位线定理中的“三角形的中位线平行于第三边”．
练习册系列答案
相关题目
如图，∠AOB=∠DOC=90°，OE平分∠AOD，反向延长射线OE至F．
（1）∠AOD和∠BOC是否互补？说明理由；
（2）射线OF是∠BOC的平分线吗？说明理由；
（3）反向延长射线OA至点G，射线OG将∠COF分成了4：3的两个角，求∠AOD．
某中学2011年投资16万元新增一批电脑，以后每年以相同的增长率进行投资，2013年投资25万元．求该学校这两年为新增电脑投资的年平均增长率．
水果店运回的苹果比梨多60kg，苹果和梨的质量比是7：5，运回的苹果和梨各有多少千克？
已知，如图：O1为x轴上一点，以O1为圆心作⊙O1交x轴于C、D两点，交y轴于M、N两点，∠CMD的外角平分线交⊙O1于点E，AB是弦，且AB∥CD，直线DM的解析式为y=3x+3．
（1）如图1，求⊙O1半径及点E的坐标．
（2）如图2，过E作EF⊥BC于F，若A、B为弧CND上两动点且弦AB∥CD，试问：BF+CF与AC之间是否存在某种等量关系？请写出你的结论，并证明．
（3）在（2）的条件下，EF交⊙O1于点G，问弦BG的长度是否变化？若不变直接写出BG的长（不写过程），若变化自画图说明理由．
今年某中学到“格林乡村公园”植树，已知该中学离公园约15km，部分学生骑自行车出发40分钟后，其余学生乘汽车出发，汽车速度是自行车速度的3倍，全体学生同时到达，设自行车的速度为vkm/h．
（1）用v分别表示自行车和汽车从学校到公园所用的时间；
（2）求v的值；
（3）植树活动完成后，由于学生比较劳累，骑自行车的学生的速度变为原来的
2
3
，汽车速度不变，为了使两批学生同时到达学校，那么骑自行的学生应该提前多少时间出发．
阅读理解：课本在研究“圆周角和圆心角的关系”时，有以下内容．
【议一议】如图1，其中O为圆心，观察圆周角∠ABC与圆心角∠AOC，它们的大小有什么关系？说说你的想法，并与同伴交流．小亮首先考虑了一种特殊情况，即∠ABC的一边BC经过圆心O（图2）．
∵∠AOC是△ABO的外角，
∴∠AOC=∠ABO+∠BAO．
∵OA=OB，
∴∠ABO=∠BAO．
∴∠AOC=2∠ABO，
即∠ABC=
1
2
∠AOC．

如果∠ABC的两边都不经过圆心O（图1，图3），那么结果会怎样？你能将图1与图3的两种情况分别转化成图2的情况去解决吗？
自主证明：请在图1和图3中选择一种情况解决上述问题（即∠ABC与∠AOC的大小关系），写出证明过程．
拓展探究：将图1中的弦AB绕点B旋转，当AB与⊙O相切时（图4），试探究∠ABC与∠BOC的大小关系？写出你的结论，并说明理由．
已知方程mx2-2（m+3）x+12=0是关于x的一元二次方程．
（1）求证：对任意不为零的实数m，方程总有两个实根．
（2）若方程的两根均为整数，且有一根大于2，求满足条件的整数m的值．
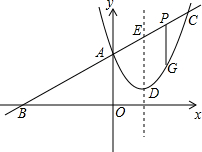如图，已知二次函数图象的顶点坐标为D（1，1），直线y=kx+m的图象与该二次函数的图象交于A、C两点，且A（0，2），直线与x轴的交点为B，满足sin∠ABO=
5
5
，点P是线段AC上一动点，且不与A，C两点重合，PG∥y轴交抛物线于点G．
（1）求k，m和这个二次函数的解析式；
（2）点E是直线BC与抛物线对称轴的交点，当△PGE∽△AOB时，求点P的坐标；
（3）若PG=
21
16
时，另外一点F在抛物线上，当S△ACF=S△ACG时，求点F的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网