题目内容
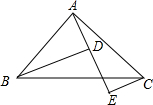 如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE.
如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE.(1)你能说明BD、DE、CE之间的数量关系吗?
(2)请你猜想△ABD满足什么条件时,BD∥CE?
考点:全等三角形的性质
专题:
分析:(1)根据全等三角形的性质求出BD=AE,AD=CE,代入求出即可;
(2)根据全等三角形的性质求出∠E=∠BDA=90°,推出∠BDE=90°,根据平行线的判定求出即可.
(2)根据全等三角形的性质求出∠E=∠BDA=90°,推出∠BDE=90°,根据平行线的判定求出即可.
解答:解:(1)BD=DE+CE‘
理由:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由是:∵△BAD≌△ACE,
∴∠E=∠ADB=90°(添加的条件是∠ADB=90°),
∴∠BDE=180°-90°=90°=∠E,
∴BD∥CE.
理由:∵△BAD≌△ACE,
∴BD=AE,AD=CE,
∴BD=AE=AD+DE=CE+DE,
即BD=DE+CE.
(2)△ABD满足∠ADB=90°时,BD∥CE,
理由是:∵△BAD≌△ACE,
∴∠E=∠ADB=90°(添加的条件是∠ADB=90°),
∴∠BDE=180°-90°=90°=∠E,
∴BD∥CE.
点评:本题考查了全等三角形的性质和平行线的判定等的应用,关键是通过三角形全等得出正确的结论,通过做此题培养了学生分析问题的能力,题型较好.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题的逆命题成立的是( )
| A、对顶角相等 |
| B、如果两个实数相等,那么它们的绝对值相等 |
| C、全等三角形的对应角相等 |
| D、两条直线平行,内错角相等 |
 如图,⊙O是△ABC的外接圆,AF平分∠BAC交BC于点E,交⊙O于点F,BD平分∠ABC交AF于点D,过点F作FH∥BC.
如图,⊙O是△ABC的外接圆,AF平分∠BAC交BC于点E,交⊙O于点F,BD平分∠ABC交AF于点D,过点F作FH∥BC.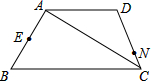 如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AB中点,请在对角线AC上找一点M使EM+MN的值最小,并求出EM+MN的最小值.
如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AB中点,请在对角线AC上找一点M使EM+MN的值最小,并求出EM+MN的最小值.


