题目内容
10.某营业厅销售的A型号手机去年销售总额为8万元,今年该型号手机每部售价预计比去年降低200元.若该型号手机的销售数量与去年相同,那么今年的销售总额将比去年减少10%.求:(1)A型号手机去年每部售价多少元?
(2)该营业厅今年计划新进一批A型号手机和新款B型号手机共60部,且B型号手机的进货数量不超过A型号手机数量的两倍.已知A型手机和B型手机的进货价格分别为1500元和1800元,计划B型手机销售价格为2400元,应如何组织进货才能使这批新近手机销售获利最多?
分析 (1)设去年A型手机每部售价x元,则今年每部售价(x-200)元,构建题意列出方程即可;
(2)设新进A型号手机a部,则新款B型号手机(60-a)部,获利y元.y=(1800-1500)a+(2400-1800)(60-a),即y=-300a+36000,求出自变量的取值范围,另一回事的性质即可解决问题;
解答 解:(1)设去年A型手机每部售价x元,则今年每部售价(x-200)元.
由题意$\frac{80000}{x}$=$\frac{80000(1-0.1)}{x-200}$,
解得x=2000,
经检验x=2000是分式方程的解,符合题意,
∴去年A型手机每部售价2000元.
(2)设新进A型号手机a部,则新款B型号手机(60-a)部,获利y元.
y=(1800-1500)a+(2400-1800)(60-a),
即y=-300a+36000,
∵60-a≤2a,
∴a≥20,
∵-300<0,
∴当a=20时,y的值最大,最大值是30000元.
点评 本题考查分式方程的应用、一次函数的应用、一元一次不等式的应用等知识,解题的关键是理解题意,正确寻找等量关系解决问题,属于中考常考题型.

练习册系列答案
相关题目
2.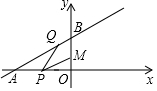 如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
 如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
20.为了了解某班同学一周的课外阅读量,任选班上15名同学进行调查,统计如表,则下列说法错误的是( )
| 阅读量(单位:本/周) | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 6 | 2 | 2 |
| A. | 中位数是2 | B. | 平均数是2 | C. | 众数是4 | D. | 方差是1.2 |
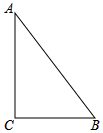 如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8.
如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.
如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则点B的对应点D的纵坐标为1.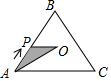 如图,在等边△ABC中,点O是中心,点P从点A出发,沿着等边三角形的边顺时针方向运动一周,则△APO的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )
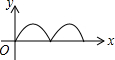
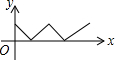
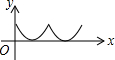
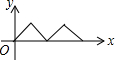
如图,在等边△ABC中,点O是中心,点P从点A出发,沿着等边三角形的边顺时针方向运动一周,则△APO的面积y与点P运动的路程x之间形成的函数关系的图象大致是( )