题目内容
2.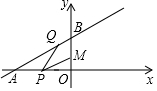 如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
如图所示,已知点M(0,2),直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,P、Q分别是线段OA,AB上的动点,则PQ+MP的最小值是3$\sqrt{3}$.
分析 如图,点M关于x轴的对称点N(0,-2),过点N作NQ⊥AB交OA于P,则NQ=PQ+PM的最小值,
根据直线y=$\frac{\sqrt{3}}{3}$x+4,得到B(0,4),∠OAB=30°,进一步得到∠ABO=60°,BN=4+2=6,解直角三角形得到结论.
解答  解:如图,点M关于x轴的对称点N(0,-2),过点N作NQ⊥AB交OA于P,
解:如图,点M关于x轴的对称点N(0,-2),过点N作NQ⊥AB交OA于P,
则NQ=PQ+PM的最小值,
∵直线y=$\frac{\sqrt{3}}{3}$x+4与两坐标轴分别交于A,B两点,
∵B(0,4),∠OAB=30°,
∴∠ABO=60°,BN=4+2=6,
∴在Rt△BQN中,QN=sin60°•BN=3$\sqrt{3}$,
∴PM+MN的最小值是 3$\sqrt{3}$.
故答案为 3$\sqrt{3}$.
点评 本题考查轴对称-最短问题、两点之间距离公式等知识,解题的关键是利用对称性找到点D、点E位置,属于中考常考题型.

练习册系列答案
相关题目
13.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.如图,是轴对称图形但不是中心对称图形的是( )
| A. |  线段 | B. |  等边三角形 | C. |  正方形 | D. |  圆 |
7.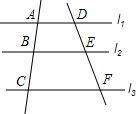 如图,若l1∥l2∥l3,则下列各式错误的是( )
如图,若l1∥l2∥l3,则下列各式错误的是( )
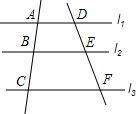 如图,若l1∥l2∥l3,则下列各式错误的是( )
如图,若l1∥l2∥l3,则下列各式错误的是( )| A. | $\frac{BC}{AC}$=$\frac{EF}{DF}$ | B. | $\frac{AB}{AC}$=$\frac{DE}{DF}$ | C. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | D. | $\frac{AB}{AC}$=$\frac{DE}{EF}$ |
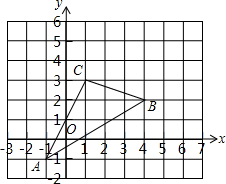 如图,△ABC在直角坐标系中,点A,B,C在格点上.
如图,△ABC在直角坐标系中,点A,B,C在格点上.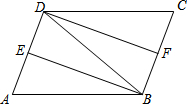 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.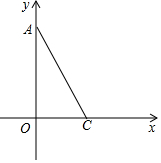 如图,在Rt△AOC中,∠A=30°,点O(0,0),C(1,0),点A在y轴正半轴上,以AC为一边作等腰直角△ACP,使得点P在第一象限.
如图,在Rt△AOC中,∠A=30°,点O(0,0),C(1,0),点A在y轴正半轴上,以AC为一边作等腰直角△ACP,使得点P在第一象限.