题目内容
1.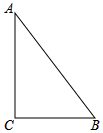 如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8.
如图,在Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,点D在斜边AB上,把△ACD沿直线CD翻折,使得点A落在同一平面内的A′处,当A′D平行Rt△ABC的直角边时,AD的长为4或8.
分析 如图1,当A′D∥BC,根据平行线的性质得到∠A′DB=∠B,根据折叠的性质得到A′D=AD,∠A′=∠A,根据三角形的面积公式得到CE=$\frac{AC•BC}{AB}$=$\frac{24}{5}$,由相似三角形的性质即可得到结论;如图2,当A′D∥AC,根据折叠的性质得到AD=A′D,AC=A′C,∠ACD=∠A′CD,根据平行线的性质得到∠A′DC=∠ACD,于是得到∠A′DC=∠A′CD,推出A′D=A′C,于是得到AD=AC=8.
解答  解:Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,
解:Rt△ABC中,∠C=90°,AB=10,sinB=$\frac{4}{5}$,
∴AC=8,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=6,
①如图1,当A′D∥BC,
∴∠A′DB=∠B,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴A′D=AD,∴∠A′=∠A,
∴∠A′+∠A′DB=90°,
∴A′C⊥AB,
∴CE=$\frac{AC•BC}{AB}$=$\frac{24}{5}$,
∴A′E=$\frac{16}{5}$,
∵A′D∥BC,
∴△A′DE∽△CBE,
∴$\frac{A′D}{BC}$=$\frac{A′E}{CE}$,即$\frac{A′D}{6}$=$\frac{\frac{16}{5}}{\frac{24}{5}}$,
∴A′D=4,
∴AD=4;
②如图2,当A′D∥AC,
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴AD=A′D,AC=A′C,∠ACD=∠A′CD,
∵∠A′DC=∠ACD,
∴∠A′DC=∠A′CD,
∴A′D=A′C,
∴AD=AC=8,
综上所述:AD的长为:4或8.
点评 本题考查了翻折变换-折叠问题,直角三角形的性质,熟练掌握折叠的性质是解题的关键.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案| A. | $\frac{30}{{({1+\frac{1}{3}})x}}-\frac{15}{x}=5$ | B. | $\frac{30}{{({1-\frac{1}{3}})x}}-\frac{15}{x}=5$ | C. | $\frac{30}{x}-\frac{15}{{({1+\frac{1}{3}})x}}=5$ | D. | $\frac{30}{x}-\frac{15}{{({1-\frac{1}{3}})x}}=5$ |
| A. |  | B. |  | C. |  | D. |  |
 如图,矩形ABCD中,BC=2AB=3,DE=2EC,∠EAF=45°,则BF的长为0.75.
如图,矩形ABCD中,BC=2AB=3,DE=2EC,∠EAF=45°,则BF的长为0.75. 某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;
某种事物经历了加热,冷却两个联系过程,折线图DEF表示食物的温度y(℃)与时间x(s)之间的函数关系(0≤x≤160),已知线段EF表示的函数关系中,时间每增加1s,食物温度下降0.3℃,根据图象解答下列问题;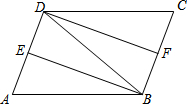 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.