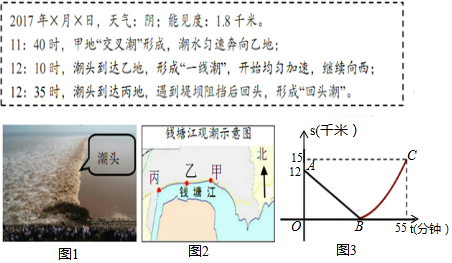
题目内容
19.如图1,已知点E,F,G,H是矩形ABCD各边的中点,AB=2.39,BC=3.57.动点M从点A出发,沿A→B→C→D→A匀速运动,到点A停止.设点M运动的路程为x,点M到四边形EFGH的某一个顶点的距离为y,如果表示y关于x的函数关系的图象如图2所示,那么四边形EFGH的这个顶点是( )
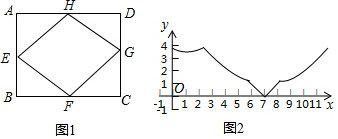
| A. | 点E | B. | 点F | C. | 点G | D. | 点H |
分析 由图象2中的图象与y轴的交点位置,可以排除E、H,再根据图象与x轴的交点位置可以排除F,由此即可判断.
解答 解:由图象2中的图象与y轴的交点位置,可以排除E、H,
再根据图象与x轴的交点位置可以排除F,
∴四边形EFGH的这个顶点是G.
故答案为C.
点评 本题主要考查了动点问题的函数图象,解题的关键是从特殊点出发解决问题,学会利用排除法解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.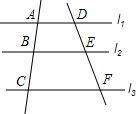 如图,若l1∥l2∥l3,则下列各式错误的是( )
如图,若l1∥l2∥l3,则下列各式错误的是( )
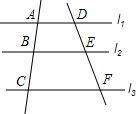 如图,若l1∥l2∥l3,则下列各式错误的是( )
如图,若l1∥l2∥l3,则下列各式错误的是( )| A. | $\frac{BC}{AC}$=$\frac{EF}{DF}$ | B. | $\frac{AB}{AC}$=$\frac{DE}{DF}$ | C. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | D. | $\frac{AB}{AC}$=$\frac{DE}{EF}$ |
11.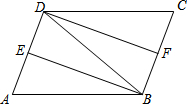 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
 如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
如图,在?ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.
8.某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.商场计划用于购进这两种商品的费用不超过9000元.
(1)写出y关于x的函数关系式:
(2)该商场至少要购进多少件甲商品?销售完这些商品.商场可获得的最大利润是多少元?
(3)实际进货时,生产厂家对甲种商品的出厂价下调m元(50<m<70)出售.且限定商场最多购70件,若商场保持同种商品的售价不变,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
| 商品名称 | 甲 | 乙 |
| 进价(元/件) | 80 | 100 |
| 售价(元/件) | 160 | 240 |
(1)写出y关于x的函数关系式:
(2)该商场至少要购进多少件甲商品?销售完这些商品.商场可获得的最大利润是多少元?
(3)实际进货时,生产厂家对甲种商品的出厂价下调m元(50<m<70)出售.且限定商场最多购70件,若商场保持同种商品的售价不变,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
 如图,矩形ABCD中,BC=2AB=3,DE=2EC,∠EAF=45°,则BF的长为0.75.
如图,矩形ABCD中,BC=2AB=3,DE=2EC,∠EAF=45°,则BF的长为0.75.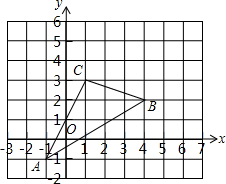 如图,△ABC在直角坐标系中,点A,B,C在格点上.
如图,△ABC在直角坐标系中,点A,B,C在格点上.