题目内容
5.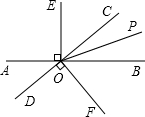 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD(1)图中除直角外,写出三对相等的角;
(2)已知∠EOC=50°,求∠POF的度数.
分析 (1)根据对顶角相等,可得①,根据角平分线的性质,可得②,根据余角的性质,可得③;
(2)根据垂直的定义以及∠EOC=50°,可得∠COB=∠EOB-∠EOC=40°.根据角平分线定义,可得∠COP=20°,那么∠POF=∠COF-∠COP=70°.
解答 解:(1)①∠AOD=∠BOC,②∠COP=BOP,③∠COE=∠BOF;
(2)∵OE⊥AB,
∴∠EOB=90°.
∵∠EOC=50°,
∴∠COB=∠EOB-∠EOC=40°.
∵OP是∠BOC的平分线,
∴∠COP=$\frac{1}{2}$∠BOC=20°.
∵OF⊥CD,
∴∠COF=90°,
∴∠POF=∠COF-∠COP=70°.
点评 本题考查了垂直的定义,对顶角、余角的性质,角平分线定义,要注意领会由垂直得直角这一要点.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 已知∠MAN和线段a,用尺规作等腰△ABC,使顶角为∠MAN,底边上的中线长为a,并写出所依据的主要定理.
已知∠MAN和线段a,用尺规作等腰△ABC,使顶角为∠MAN,底边上的中线长为a,并写出所依据的主要定理. 某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元,每天可售出40件,若每件降价10元,则每天多售出10件,请根据以上信息解答下列问题:
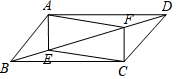 如图,在平行四边形ABCD中,E、F为对角线BD上两点,BE=DF,连接AE、EC、CF、FA.
如图,在平行四边形ABCD中,E、F为对角线BD上两点,BE=DF,连接AE、EC、CF、FA.