题目内容
2.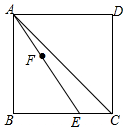 如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则$\frac{BF}{FG}$的值为1或$\frac{12}{13}$.
如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则$\frac{BF}{FG}$的值为1或$\frac{12}{13}$.
分析 分两种情形:①当G在AD边上时,②当G′在CD上时分别求解即可;
解答 解:①当G在AD边上时,∵AE=BG,AB=AB,∠BAG=∠ABE=90°,
∴△ABG≌△BAE,
∴AG=BE,
∵AG∥BE,
∴$\frac{BF}{FG}$=$\frac{BE}{AG}$=1.
②当G′在CD上时,易证△ABE≌△BCG′,
∴∠BAE=∠CBG′,
∵∠CBG′+∠ABF′=90°,
∴∠BAE+∠ABF′=90°,
∴∠AF′B=90°,
∴BG′⊥AE,
∵AB=8.BE=6,
∴AE=BG′=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵$\frac{1}{2}$•AB•BE=$\frac{1}{2}$•AE•BF′,
∴BF′=$\frac{24}{5}$,F′G′=10-$\frac{24}{5}$=$\frac{26}{5}$,
∴$\frac{BF′}{F′G′}$=$\frac{\frac{24}{5}}{\frac{26}{5}}$=$\frac{12}{13}$
故答案为1或$\frac{12}{13}$.
点评 本题考查相似三角形的判定和性质、全等三角形的判定和性质、正方形的性质、勾股定理平行线分线段成比例定理等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.

练习册系列答案
相关题目
11.某商场自今年二月份起销售额连续增长,二月份和三月份的平均增长率为a%,则三月份的销售额比一月份增长了( )
| A. | 2a% | B. | 1+2a% | C. | (2+a%)a% | D. | (1+a%)2 |
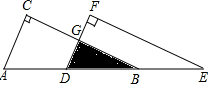 如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.
如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.
 如图,正方形ABCD和CEFG的边长分别为m、n,试用m、n的代数式表示三角形BDF的面积S.
如图,正方形ABCD和CEFG的边长分别为m、n,试用m、n的代数式表示三角形BDF的面积S.