题目内容

12．如果平行四边形一组邻角的度数比为1：2，那么这个四边形最大内角的度数为120°．

分析 首先设平行四边形中两个内角的度数分别是x°，2x°，由平行四边形的邻角互补，即可得方程x+2x=180，继而求得答案．

解答 解：设平行四边形中两个内角的度数分别是x°，2x°，
则x+2x=180，
解得：x=60，
∴其中较大的内角是：120°．
故答案为：120°．

点评 此题考查了平行四边形的性质，注意平行四边形的邻角互补．

练习册系列答案
相关题目
2．$\sqrt{3}$•$\sqrt{\frac{6}{x}}$是整数，那么x是（　　）
A．6和3B．3和1C．2和18D．只有18
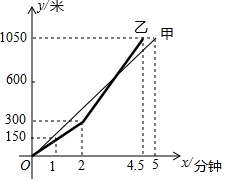3．百舸竞渡，激情飞扬．端午节期间，某地举行龙舟比赛．甲、乙两支龙舟队在比赛时路程y（米）与时间x（分钟）之间的函数图象如图所示．根据图象回答下列问题：
（1）1.5分钟时，哪支龙舟队处于领先位置？
（2）在这次龙舟赛中，哪支龙舟队先到达终点？先到达多少时间？
（3）求乙队加速后，路程y（米）与时间x（分钟）之间的函数关系式．
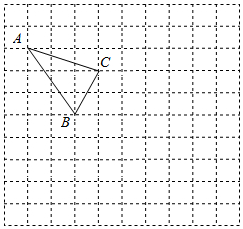20．如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点）ABC的顶点A，C的坐标分别为（-4，4），（-1，3）．
（1）请在如图所示的网格平面内画出平面直角坐标系；
（2）把三角形ABC先向右平移5个单位长度，再向下平移3个单位长度得到三角形A′B′C′，且点A，B，C的对应点分别为A′，B′，C′，请你在图中画出三角形A′B′C′；
（3）求三角形ABC的面积．
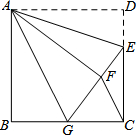7．如图所示，在正方形ABCD中，AB=12，点E在CD边上，且CD=3DE，将△ADE沿着AE 对折至△AFE，延长EF交边BC与点G，连接AG，CF．有下列结论①△ABG≌△AFG  ②BG=GC  ③AG∥CF ④S△FGC=12，正确的是①②③（填序号）
17．（1）已知2x-3的立方根是5，求x的平方根；
（2）若a+2和2a-11都是一个正数的平方根，求a及这个正数．
4．已知 $\sqrt{x+1}$+$\sqrt{y-x}$=0，求x和y的值．
1．尺规作图：
已知：△ABC，
（1）求作：△DEF，使△DEF≌△ABC．
（2）根据你的作法，说明△DEF≌△ABC的理由．
2．圆锥的体积是120立方分米，底面积是10平方分米，高是（　　）分米．
A．12B．24C．36D．48

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网