题目内容
7.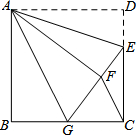 如图所示,在正方形ABCD中,AB=12,点E在CD边上,且CD=3DE,将△ADE沿着AE 对折至△AFE,延长EF交边BC与点G,连接AG,CF.有下列结论①△ABG≌△AFG ②BG=GC ③AG∥CF ④S△FGC=12,正确的是①②③(填序号)
如图所示,在正方形ABCD中,AB=12,点E在CD边上,且CD=3DE,将△ADE沿着AE 对折至△AFE,延长EF交边BC与点G,连接AG,CF.有下列结论①△ABG≌△AFG ②BG=GC ③AG∥CF ④S△FGC=12,正确的是①②③(填序号)
分析 由正方形的性质和折叠的性质得出AB=AF,∠AFG=90°,由HL证明Rt△ABG≌Rt△AFG,得出①正确;
设BG=FG=x,则CG=12-x.由勾股定理得出方程,解方程求出BG,得出GC,即可得出②正确;
由全等三角形的性质和三角形内角和定理得出∠AGB=∠AGF=∠GFC=∠GCF,得出AG∥CF,即可得出③正确;
通过计算三角形的面积得出④错误;即可得出结果.
解答 解:①正确.理由如下:
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=12,∠B=∠GCE=∠D=90°,
由折叠的性质得:AF=AD,∠AFE=∠D=90°,
∴∠AFG=90°,AB=AF,
在Rt△ABG和Rt△AFG中,
$\left\{\begin{array}{l}{AG=AG}\\{AB=AF}\end{array}\right.$,
∴Rt△ABG≌Rt△AFG(HL);
②正确.理由如下:
由题意得:EF=DE=$\frac{1}{3}$CD=4,设BG=FG=x,则CG=12-x.
在直角△ECG中,根据勾股定理,得(12-x)2+82=(x+4)2,
解得:x=6,
∴BG=6,
∴GC=12-6=6,
∴BG=GC;
③正确.理由如下:
∵CG=BG,BG=GF,
∴CG=GF,
∴△FGC是等腰三角形,∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG,
∴∠AGB=∠AGF,∠AGB+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GFC=2∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,
∴AG∥CF;
④错误;理由如下:
∵S△GCE=$\frac{1}{2}$GC•CE=$\frac{1}{2}$×6×8=24,
∵GF=6,EF=4,△GFC和△FCE等高,
∴S△GFC:S△FCE=3:2,
∴S△GFC=$\frac{3}{5}$×24=$\frac{72}{5}$≠12.
故④不正确.
∴正确的个数有①②③.
故答案为:①②③.
点评 本题考查的是翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算等知识;本题综合性强,有一定的难度.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案| A. | a6•a=a7 | B. | (-3ab)2=6a2b2 | C. | a6÷a=a6 | D. | (-bc)4÷(-bc)2=-b2c2 |
 如图,已知公路AB和公路CD互相平行,现要在两条公路之间修建一条贯通AB和CD的公路DE和EF,若测得∠DEF=95°,∠D=45°,那么∠ABF的度数为( )
如图,已知公路AB和公路CD互相平行,现要在两条公路之间修建一条贯通AB和CD的公路DE和EF,若测得∠DEF=95°,∠D=45°,那么∠ABF的度数为( )| A. | 135° | B. | 130° | C. | 125° | D. | 120° |
| A. | 1,2,3 | B. | 4,5,6 | C. | $\sqrt{3}$,2,$\sqrt{5}$ | D. | 6,8,10 |
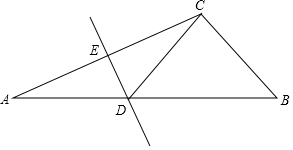 如图,在△ABC中,∠ACB=111°,AC边上的垂直平分线交AB于点D,交AC边于点E,连接CD.
如图,在△ABC中,∠ACB=111°,AC边上的垂直平分线交AB于点D,交AC边于点E,连接CD.