题目内容
17．（1）已知2x-3的立方根是5，求x的平方根；（2）若a+2和2a-11都是一个正数的平方根，求a及这个正数．
分析 （1）利用立方根定义求出x的值，即可确定出x的平方根；
（2）根据一个正数的算术平方根的和为零，可得关于a的一元一次方程，根据解一元一次方程，可得a，根据平方运算，可得被开方数．
解答 解：（1）根据题意得：2x-3=125，
解得：x=64，
则64的平方根是8或-8；
（2）一个正数的平方根是a+2和2a-11，得
a+2+2a-11=0．
解得a=3，
（a+2）2=（3+2）2=52=25，
故这个正数为25．
点评 此题考查了平方根，熟练掌握定义是解本题的关键．（2）利用一个正数的平方根互为相反数得出关于a的一元一次方程是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
一辆货车从A地运货到240km的B地，卸货后返回A地，如图中实线是货车离A地的路程y（km）关于出发后的时间x（h）之间的函数图象．货车出发时，正有一个自行车骑行团在AB之间，距A地40km处，以每小时20km的速度奔向B地．
5．某校随机抽查了10名参加2017年我市初中学业水平考试学生的体育成绩，得到的结果如表：
下列说法中，正确的是（ ）
| 成绩/分 | 56 | 57 | 58 | 59 | 60 |
| 人数 | 1 | 2 | 1 | 2 | 4 |
| A． | 这10名学生体育成绩的中位数为58 | B． | 这10名学生体育成绩的平均数为58 | ||
| C． | 这10名学生体育成绩的众数为60 | D． | 这10名学生体育成绩的方差为60 |
2．某种禽流感病毒变异后的直径为0.00000018米，0.00000018米用科学记数法表示为（ ）
| A． | 1.8×10-5米 | B． | 0.18×10-6米 | C． | 1.8×10-7米 | D． | 18×10-8米 |
9．
如图，在菱形ABCD中，∠ABC=120°，BD=4，则菱形ABCD的面积是（ ）
如图，在菱形ABCD中，∠ABC=120°，BD=4，则菱形ABCD的面积是（ ）| A． | 4$\sqrt{3}$ | B． | 8 | C． | 8$\sqrt{3}$ | D． | 16 |
6．
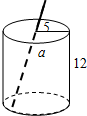如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，已知一条到达底部的直吸管在罐内部分的长度为a，若直吸管在罐外部分还剩余3，则吸管的总长度b（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）
如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，已知一条到达底部的直吸管在罐内部分的长度为a，若直吸管在罐外部分还剩余3，则吸管的总长度b（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）| A． | 12≤b≤13 | B． | 12≤b≤15 | C． | 13≤b≤16 | D． | 15≤b≤16 |