题目内容
2．$\sqrt{3}$•$\sqrt{\frac{6}{x}}$是整数，那么x是（ ）| A． | 6和3 | B． | 3和1 | C． | 2和18 | D． | 只有18 |
分析 根据二次根式的运算法则即可求出答案．
解答 解：原式=3$\sqrt{\frac{2}{x}}$，
∵$\sqrt{3}$•$\sqrt{\frac{6}{x}}$是正数，
∴$\sqrt{\frac{2}{x}}$=1或$\sqrt{\frac{2}{x}}$=$\frac{1}{3}$，
解得：x=2或x=18，
故选（C）
点评 本题考查二次根式的运算，解题的关键是熟练运用二次根式的性质，本题属于基础题型．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
丰县红富士苹果是江苏徐州丰县特产，某水果超市，营销员的个人收入与他每月的销售量一闪函数关系，其图象如下图所示，请你根据图象中提供的信息，解答以下问题．
13．
如图，∠AOC和∠BOD都是直角．如果∠DOC=28°，则下列判断错误的是（ ）
如图，∠AOC和∠BOD都是直角．如果∠DOC=28°，则下列判断错误的是（ ）| A． | ∠AOD=∠BOC | B． | ∠AOB=148° | ||
| C． | ∠AOB+∠DOC=180° | D． | 若∠DOC变小，则∠AOB变大 |
17．下列计算正确的是（ ）
| A． | a6•a=a7 | B． | （-3ab）2=6a2b2 | C． | a6÷a=a6 | D． | （-bc）4÷（-bc）2=-b2c2 |
一辆货车从A地运货到240km的B地，卸货后返回A地，如图中实线是货车离A地的路程y（km）关于出发后的时间x（h）之间的函数图象．货车出发时，正有一个自行车骑行团在AB之间，距A地40km处，以每小时20km的速度奔向B地．
11．
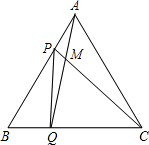如图，点P，Q是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都是1cm/s，连接AQ，CP交于点M，则在P，Q运动的过程中，下列结论错误的是（ ）
如图，点P，Q是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都是1cm/s，连接AQ，CP交于点M，则在P，Q运动的过程中，下列结论错误的是（ ）| A． | △ABQ≌CAP | B． | ∠CMQ的度数不变，始终等于60° | ||
| C． | BP=CM | D． | △PBQ有可能为直角三角形 |