题目内容
6.某超市店庆,推出如下购物优惠方案:(1)一次性购物在100元(不含100元)以内时,不享受优惠;
(2)一次性购物在100元(含100元)以上,300元(不含300元)以内时,一律享受九折的优惠;
(3)一次性购物在300元(含300元)以上时,一律享受八折的优惠.
小明在本超市两次购物分别付款80元、252元.如果改成在本超市一次性购买与上两次完全相同的商品,则应付款( )
| A. | 332元 | B. | 288元 | C. | 288元或316元 | D. | 288元或332元 |
分析 由80<100×0.9可得出第一次购买的商品价值为80元,由300×0.8<252<300×0.9可得出第二次购买的商品价值可能小于300元也可能大于300元,设第二次购买的商品价值为x元,根据应付款=商品价值×折扣率即可得出关于x的一元一次方程,解之即可得出x的值,由此即可求出两次购买的商品总价值,再用其×0.8即可得出若在本超市一次性购买与上两次完全相同的商品,应付款金额.
解答 解:∵100×0.9=90(元),80<90,
∴第一次购买的商品价值为80元.
∵300×0.8=240(元),300×0.9=270(元),270>252>240,
∴第二次购买的商品价值可能小于300元也可能大于300元.
设第二次购买的商品价值为x元,
当100<x<300时,有0.9x=252,
解得:x=280;
当x>300时,有0.8x=252,
解得:x=315.
∴两次购买的商品总价值为80+280=360(元)或80+315=395(元).
∵360×0.8=288(元),395×0.8=316(元),
∴在本超市一次性购买与上两次完全相同的商品,则应付款288元或316元.
故选C.
点评 本题考查了一元一次方程的应用,根据数量关系应付款=商品价值×折扣率确定第二次购买的商品价值可能小于300元也可能大于300元是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
11.实数a,b,c满足a2+6b=-17,b2+8c=-23,c2+2a=14,则a+b+c的值是( )
| A. | -6 | B. | -7 | C. | -8 | D. | -9 |
18.下列不等式中,正确的个数是( )
-4$\frac{2}{3}$>-4.7,-$\frac{12}{23}$<-$\frac{6}{11}$,-0.$\stackrel{•}{2}$>-0.22,-0.01<-$\frac{1}{100}$.
-4$\frac{2}{3}$>-4.7,-$\frac{12}{23}$<-$\frac{6}{11}$,-0.$\stackrel{•}{2}$>-0.22,-0.01<-$\frac{1}{100}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.若m是任意实数,则点A(m2+1,-4)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
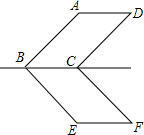 如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F.
如图,?ABCD与?EBCF关于BC所在直线对称,∠ABE=90°,求∠F.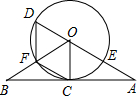 如图,直线AB经过⊙O上的C点,OA、OB分别与⊙O相于E点和F点,且EA=FB,CA=CB,AO的延长线交⊙O于点D.
如图,直线AB经过⊙O上的C点,OA、OB分别与⊙O相于E点和F点,且EA=FB,CA=CB,AO的延长线交⊙O于点D.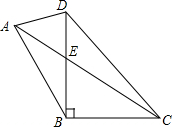 如图,在四边形ABCD中,∠DBC=90°,∠ABD=30°,∠ADB=75°,AC与BD交于点E,若CE=2AE=4$\sqrt{3}$,则DC的长为6$\sqrt{2}$.
如图,在四边形ABCD中,∠DBC=90°,∠ABD=30°,∠ADB=75°,AC与BD交于点E,若CE=2AE=4$\sqrt{3}$,则DC的长为6$\sqrt{2}$.