题目内容
7.关于x、y的方程组$\left\{\begin{array}{l}{ax+2by=4}\\{3x+2y=4}\end{array}\right.$与$\left\{\begin{array}{l}{2x-3y=7}\\{bx+(a-1)y=4}\end{array}\right.$的解相同,求a与b的值.分析 联立不含a与b的方程组成方程组,求出方程组的解得到x与y的值,代入剩下两个方程求出a与b的值即可.
解答 解:联立得:$\left\{\begin{array}{l}{3x+2y=4①}\\{2x-3y=7②}\end{array}\right.$,
①×3+②×2得:13x=26,
解得:x=2,
把x=2代入①得:y=-1,
把$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$代入得:$\left\{\begin{array}{l}{a-b=2}\\{a-2b=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=7}\\{b=5}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.用加减消元法解二元一次方程组$\left\{\begin{array}{l}{2x-3y=7①}\\{5x-3y=-2②}\end{array}\right.$,由①-②可得的方程为( )
| A. | 3x=5 | B. | -3x=9 | C. | -3x-6y=9 | D. | 3x-6y=5 |
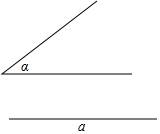 如图,已知∠α和线段a,求作△ABC,使BC=a,∠B=∠C=$\frac{1}{2}$α(只保留作图痕迹,不要求写出作法)
如图,已知∠α和线段a,求作△ABC,使BC=a,∠B=∠C=$\frac{1}{2}$α(只保留作图痕迹,不要求写出作法) 如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图.
如图所示是由几个小立方体所组成几何体的俯视图,小正方形中的数字表示在该位置的小立方体的个数,请画出这个几何体的主视图、左视图. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc<0;③8a+c>0;④9a+3b+c<0;⑤m(am+b)≥a+b(m取任意实数)其中,正确的结论个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2-4ac>0;②abc<0;③8a+c>0;④9a+3b+c<0;⑤m(am+b)≥a+b(m取任意实数)其中,正确的结论个数是( ) 如图,AB为⊙O的直径,ED切⊙O于点C,过点A作AF⊥ED于点F,交⊙O于点G,连接AC;
如图,AB为⊙O的直径,ED切⊙O于点C,过点A作AF⊥ED于点F,交⊙O于点G,连接AC;