Question

5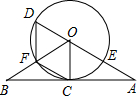．如图，直线AB经过⊙O上的C点，OA、OB分别与⊙O相于E点和F点，且EA=FB，CA=CB，AO的延长线交⊙O于点D．
（1）求证：AB是⊙O的切线；
（2）若DE=10，四边形CODF是菱形，求AB及AE的长
（3）在（2）的条件下求菱形CODF的面积．

Answer 1

分析 （1）只要证明△OCB≌△OCA，推出∠OCB=∠OCA=$\frac{1}{2}$×180°=90°，即OC⊥AB，由此即可证明．
（2）由四边形CODF是菱形，推出OC=CF=OF，推出△OCF是等边三角形，推出∠BOC=60°，由∠OCB=90°，∠OBC=30°，由此即可解决问题．
（3）等边三角形的面积=$\frac{\sqrt{3}}{4}$a²（a是等边三角形的边长），根据题意菱形的面积是两个等边三角形的面积和，由此即可解决问题．

解答 解：（1）∵OF=OE，BF=AE，
∴OB=OA，
在△OCB和△OCA中，
$\left\{\begin{array}{l}{OC=OC}\\{OB=OA}\\{CB=CA}\end{array}\right.$，
∴△OCB≌△OCA，
∴∠OCB=∠OCA=$\frac{1}{2}$×180°=90°，
∴OC⊥AB，
∴AB是⊙O的切线．

（2）∵四边形CODF是菱形，
∴OC=CF=OF，
∴△OCF是等边三角形，
∴∠BOC=60°，∵∠OCB=90°，
∴∠OBC=30°
∵DE=10，
∴OC=OE=5，
∴OB=OA=2OC=10，AB=2BC=10$\sqrt{3}$，AE=OA-OE=5．

（3）∵△OFC，△ODF都是等边三角形，边长为5，
∴菱形DFCO的面积=2×$\frac{\sqrt{3}}{4}$×（5²）=$\frac{50}{4}$$\sqrt{3}$．

点评 本题考查圆综合题、菱形的性质、全等三角形的判定和性质、等边三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，本题的突破点是发现△OFC，△ODF是等边三角形，属于中考常考题型．