题目内容
3.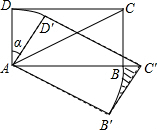 如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )
如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )| A. | $\frac{\sqrt{3}}{2}$$-\frac{π}{4}$ | B. | $\frac{\sqrt{3}}{2}-\frac{π}{12}$ | C. | $\frac{\sqrt{3}}{2}-\frac{π}{2}$ | D. | $\frac{\sqrt{3}}{2}-\frac{π}{6}$ |
分析 首先根据题意利用锐角三角函数关系得出旋转角的度数,进而求出S△AB′C′,S扇形BAB′,即可得出阴影部分面积.
解答 解:∵在矩形ABCD中,AB=$\sqrt{3}$,AD=1
∴tan∠CAB=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,AB=CD=$\sqrt{3}$,AD=BC=1,
∴∠CAB=30°,
∴∠BAB′=30°,
∴S△AB′C′=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
S扇形BAB′=$\frac{30π×(\sqrt{3})^{2}}{360}$=$\frac{π}{4}$,
S阴影=S△AB′C′-S扇形BAB′=$\frac{\sqrt{3}}{2}-\frac{π}{4}$.
故选:A.
点评 此题主要考查了矩形的性质以及旋转的性质以及扇形面积公式等知识,得出旋转角的度数是解题关键.

练习册系列答案
相关题目
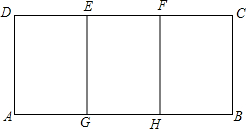 如图,矩形ABCD能分成三个全等的小矩形,且每个小矩形都与矩形ABCD相似,已知AD=1,求AB的长.
如图,矩形ABCD能分成三个全等的小矩形,且每个小矩形都与矩形ABCD相似,已知AD=1,求AB的长.
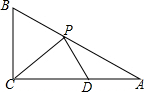 如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=5,点P,D分别是线段AB,AC上的两个动点,则PC+PD的最小值为8.
如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=5,点P,D分别是线段AB,AC上的两个动点,则PC+PD的最小值为8.