题目内容
19.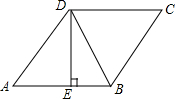 如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20.
如图,在菱形ABCD中,已知DE⊥AB,AE:AD=3:5,BE=2,则菱形ABCD的面积是20.
分析 设AE=3x,则AD=5x,则BE=AD-AE=2x,再由BE=2得出x的值,根据勾股定理求出DE的长,由菱形的面积公式即可得出结论.
解答 解:∵AE:AD=3:5,BE=2,
∴设AE=3x,则AD=5x,
∴BE=AD-AE=2x=2,解得x=1,
∴AD=AB=5,DE=3.
∵DE⊥AB,
∴DE=$\sqrt{{AD}^{2}-{AE}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴S菱形ABCD=AB•DE=5×4=20.
故答案为:20.
点评 本题考查的是菱形的性质,熟知菱形的四条边都相等及勾股定理是解答此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
10.菱形的对角线AC=8cm,BD=6cm,AC、BD相交于点O,则点O到任一边中点的距离为( )
| A. | 2.5cm | B. | 2.4cm | C. | 5cm | D. | 3cm |
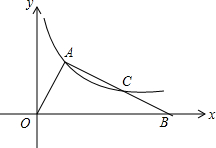 如图,直角△AOB的斜边OB在x轴正半轴上,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=BC,OA=3,则k=3$\sqrt{2}$.
如图,直角△AOB的斜边OB在x轴正半轴上,双曲线y=$\frac{k}{x}$(x>0)经过点A,交AB于点C,且AC=BC,OA=3,则k=3$\sqrt{2}$. 如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.
如图,A是函数y=$\frac{k}{x}$上一点.AB⊥x轴于B点,若S△AOB=4.
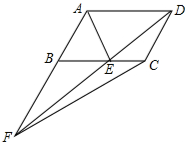 如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.
如图,在?ABCD中,点E在BC上,AE平分∠BAD,且AB=AE,连接DE并延长与AB的延长线交于点F,连接CF,若AB=1cm,则△CEF面积是$\frac{\sqrt{3}}{4}$cm2.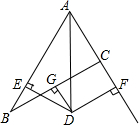 如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.
如图,在△ABC中,AB=8,AC=4,G为BC的中点,DG⊥BC交∠BAC的平分线AD于D,DE⊥AB于E,DF⊥AC于F交AC的延长线于F.