题目内容
13. 如图所示的桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,分别求出两条钢缆所在抛物线的解析式.
如图所示的桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,分别求出两条钢缆所在抛物线的解析式.
分析 根据图象可以看出右侧的图象顶点为(20,0),过(0,8),运用待定系数法可求出解析式,左侧的函数图象与右侧的关于y轴对称,根据对称性可写出左侧函数解析式.
解答 解:∵右侧的图象顶点为(20,0),过(0,8),
设y右=a(x-20)2,代入(0,8)得:
400a=8
∴a=$\frac{1}{50}$,
∴y右=$\frac{1}{50}$(x-20)2,
∵左侧的函数图象与右侧的关于y轴对称,
∴y左=$\frac{1}{50}$(x+20)2.
点评 本题主要考查了待定系数法求二次函数表达式,熟练掌握二次函数求解析式的方法是解决问题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
4.已知$\overrightarrow{m}$=3$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$,$\overrightarrow{n}$=$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{a}$,那么$\overrightarrow{m}$-4$\overrightarrow{n}$等于( )
| A. | 2$\overrightarrow{a}$-$\frac{8}{3}$$\overrightarrow{b}$ | B. | 4$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | C. | 2$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | D. | 4$\overrightarrow{a}$-$\frac{8}{3}$$\overrightarrow{b}$ |
8.某商场经理接到的采购部和销售部的两个电话,根据电话内容完成下列问题:
(1)写出该商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式,并指出自变量x的取值范围.
(2)当销售价为多少元时,每天的销售利润最大?最大利润为多少?
(1)写出该商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式,并指出自变量x的取值范围.
(2)当销售价为多少元时,每天的销售利润最大?最大利润为多少?
| 采购部 | 经理,这里有一批商品以每件42元购回 |
| 销售部 | 经理,以每件42元购回的商品,每天的销售量t(件)与每件的销售价x(元)呈现的关系是:t=-3x+204 |
3. 如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )
如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )
 如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )
如图,已知∠3=∠4,要得到AB∥CD,需要添加的条件是( )| A. | ∠1=∠4 | B. | ∠3=∠2 | C. | ∠1=∠2 | D. | ∠1与∠2互补 |
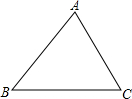 如图,在△ABC中,AB=9cm,AC=6cm,D是线段AB的一点,AD=3,点E时线段AC上的任意一点,当AE为多少时,△ADE与△ABC相似?
如图,在△ABC中,AB=9cm,AC=6cm,D是线段AB的一点,AD=3,点E时线段AC上的任意一点,当AE为多少时,△ADE与△ABC相似?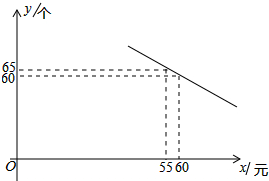 某体育用品商店试销一款成本为50元的排球,规定①试销售期三天;②试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
某体育用品商店试销一款成本为50元的排球,规定①试销售期三天;②试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.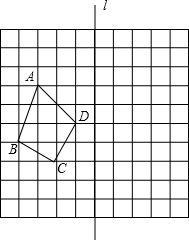 如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.