题目内容
1.某超市经销一种销售成本为每件20元的商品,据市场调查分析,如果按每件25元销售,一周能售出1000件;若销售单价每涨1元,每周销售量就减少20件.设销售单价为x元(x≥25),一周的销售量为y件.(1)写出y与x之间的函数关系式(标明x的取值范围);
(2)设一周的销售利润为S元,写出S与x之间的函数关系式;
(3)在超市对该种商品投入不超过10000元的情况下,使得一周的销售利润达到9000元,销售单价应定为多少.
分析 (1)根据题意一周能售出1000件,若销售单价每涨1元,每周销量就减少10件,可得y=1000-20(x-25);
(2)利用一周的销售量×每件销售利润=一周的销售利润列出一周的销售利润为S,写出S与x的函数关系式;
(3)令s=9000,解方程求解,根据商品投入不超过10000元的情况下求出x的取值.
解答 解:(1)由题意得:y=1000-20(x-25)=1500-20x(25≤x≤75);
(2)S=(x-20)(1500-20x)=-20x2+1900x-30000;
(3)由题意得:-20x2+1900x-30000=9000
x2-95x+1950=0
即(x-65)(x-30)=0
x1=65,x2=30,
当x=65时,成本=20×(1500-20×65)=4000<10000符合要求,
当x=30时,成本=20×(1500-20×30)=18000>10000不符合要求,舍去.
答:销售单价应定为65元,才能使得一周销售利润达到9000元的同时,投入不超过10000元.
点评 此题主要考查了二次函数的应用,准确分析题意,列出二次函数关系式是解题关键.

练习册系列答案
相关题目
 已知如图,在△ABC中,∠ACB的平分线CE与外角∠DAB的平分线AE交于点E,求证:∠B=2∠E.
已知如图,在△ABC中,∠ACB的平分线CE与外角∠DAB的平分线AE交于点E,求证:∠B=2∠E. 如图所示的桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,分别求出两条钢缆所在抛物线的解析式.
如图所示的桥梁的两条钢缆具有相同的抛物线形状,按照图中的直角坐标系,分别求出两条钢缆所在抛物线的解析式. 如图,∠C=90°,∠1=∠2,若BC=9,BD=5,则D到AB的距离为4.
如图,∠C=90°,∠1=∠2,若BC=9,BD=5,则D到AB的距离为4.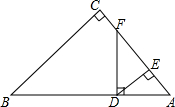 如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.
如图所示,在△ABC中,∠C=90°,D是AB上一点,DF⊥AB交AC于点F,DE⊥AC,垂足为点E.若EF:CF=2:1,DE=2,BD=6$\sqrt{5}$,求BC的长.