题目内容
1.已知方程组$\left\{\begin{array}{l}{ax+5y=15①}\\{4x-by=-2②}\end{array}\right.$由于甲看错了方程①中的a,得到方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$,乙看错了方程②中的b,得到方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$,试求出a,b的值.分析 根据方程组的解的定义,$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$应满足方程②,$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$应满足方程①,将它们分别代入方程②①,就可得到关于a,b的方程,解得a,b的值.
解答 解:甲看错了①式中x的系数a,解得$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$,但满足②式的解,所以-12+b=-2,解得:b=10;
同理乙看错了②式中y的系数b,解得$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$,满足①式的解,所以5a+10=15,解得:a=1.
点评 此题主要考查了二元一次方程组解的定义,解决本题的关键是二元一次方程组解的定义.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{8}$-2$\sqrt{2}$=0 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | (2-$\sqrt{5}$)(2+$\sqrt{5}$)=1 |
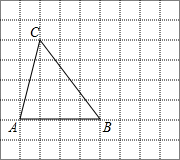 作图题:在方格纸中,将△ABC向右平移4个单位得到△A1B1C1
作图题:在方格纸中,将△ABC向右平移4个单位得到△A1B1C1