题目内容
10.如图,点C在以AB为直径的⊙O上,∠CBA=30°,点D在AB上由点A开始向点B运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.(1)如果CD⊥AB,求证:EF为⊙O的切线;
(2)求证:CE=CF;
(3)如果点F恰好落在弧BC上,请在备用图中画出图形,探究并证明此时EF与AB的关系.
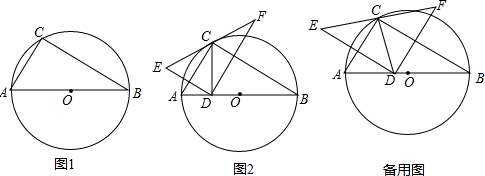
分析 (1)连接OC,先证明△AOC是等边三角形,得出∠OCA=60°,再求出∠OCD=∠DCA=30°,由轴对称的性质得出∠ECA=∠DCA=30°,求出∠ECO=90°,即可得出结论;
(2)由轴对称的性质得出CE=CD,再求出∠CDF=∠F,得出CD=CF,即可得出结论;
(3)当点F恰好落在$\widehat{BC}$上时,点D与点O重合,由(2)得CE=OC,CF=OC,得出EF=2OC=AB,△OCF是等边三角形,得出∠F=∠COF=60°,再求出∠BOF=60°,得出∠F=∠BOF,即可得出EF∥AB.
解答 (1)证明:连接OC,如图2所示:
∵∠ACB=90°,∠CBA=30°,
∴∠CAB=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴∠OCA=60°,
∵CD⊥AB,
∴∠OCD=∠DCA=30°,
∵点E与点D关于AC对称,
∴CD=CE,
∴∠ECA=∠DCA=30°,
∴∠ECO=60°+30°=90°,
∴EF为⊙O的切线;
(2)证明:∵点E与点D关于AC对称,
∴CE=CD,
∴∠ECA=∠DCA,
又∵DF⊥DE,
∴∠CDF=90°-∠CDE=90°-∠E=∠F,
∴CD=CF,
∴CE=CF;
(3)解:如图3所示: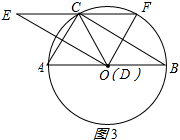 EF=AB,EF∥AB;理由如下:
EF=AB,EF∥AB;理由如下:
当点F恰好落在$\widehat{BC}$上时,此时点D与点O重合,
由(2)得CE=OC,CF=OC,
∴EF=2OC=AB,△OCF是等边三角形,
∴∠F=∠COF=60°,
∵OB=OC,
∴∠OCB=∠B=30°,
∴∠BOC=120°,
∴∠BOF=60°,
∴∠F=∠BOF,
∴EF∥AB.
点评 本题是圆的综合题目,考查了切线的判定、轴对称的性质、等腰三角形的判定、等边三角形的判定与性质、平行线的判定等知识,本题难度较大,综合性强,特别是(3)中,需要画出图形,得出点D与点O重合,证明三角形是等边三角形才能得出结果.

 如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )
如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )| A. | S=AD•CE | B. | S>AD•CE | C. | S<AD•CE | D. | 无法确定 |
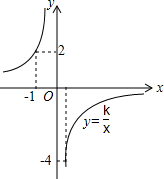 反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )
反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )| A. | -4≤x<0或0<x<2 | B. | x<-1或x≥$\frac{1}{2}$ | C. | -1<x≤$\frac{1}{2}$ | D. | -1<x<0或0<x≤$\frac{1}{2}$ |
| A. | y=x2+2 | B. | y=x2-2 | C. | y=(x+2)2 | D. | y=(x-2)2 |
| A. | 该卡片标号不大于5 | B. | 该卡片标号大于5 | ||
| C. | 该卡片标号是奇数 | D. | 该卡片标号是3 |
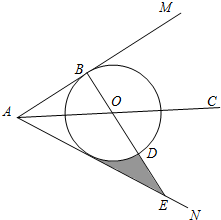 如图,AC平分∠MAN,点O在射线AC上,以点O为圆心,半径为1的⊙O与AM相切于点B,连接BO并延长交⊙O于点D,交AN于点E.
如图,AC平分∠MAN,点O在射线AC上,以点O为圆心,半径为1的⊙O与AM相切于点B,连接BO并延长交⊙O于点D,交AN于点E.