题目内容
13.请写出一个以$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$为解的二元一次方程组$\left\{\begin{array}{l}{x+y=6}\\{x-y=4}\end{array}\right.$.分析 根据二元一次方程组的解的定义写出即可.
解答 解:二元一次方程组$\left\{\begin{array}{l}{x+y=6}\\{x-y=4}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{x+y=6}\\{x-y=4}\end{array}\right.$
点评 本题考查了二元一次方程组的解的定义,是基础题,比较简单,写出的方程组越简单越好.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
18. 如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )
如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )
 如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )
如图,D、E分别为△ABC的边AB、AC上的点,△ACD与△BCD的周长相等,△ABE与△CBE的周长相等,记△ABC的面积为S.若∠ACB=90°,则AD•CE与S的大小关系为( )| A. | S=AD•CE | B. | S>AD•CE | C. | S<AD•CE | D. | 无法确定 |
2.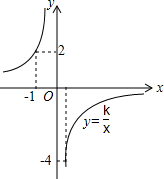 反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )
反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )
 反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )
反比例函数y=$\frac{k}{x}$的图象如图所示,根据图中的信息可得到不等式组$\left\{\begin{array}{l}{\frac{k}{x}≥-4}\\{\frac{k}{x}<2}\end{array}\right.$的解集为( )| A. | -4≤x<0或0<x<2 | B. | x<-1或x≥$\frac{1}{2}$ | C. | -1<x≤$\frac{1}{2}$ | D. | -1<x<0或0<x≤$\frac{1}{2}$ |
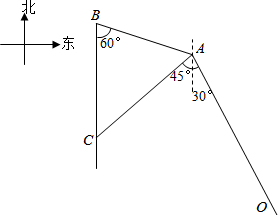 背景材料:近年来由于世界各国大力发展海洋经济、加强海洋能力开发,海洋争端也呈上升趋势.为增强海洋执法能力、维护海洋领土,近期我国多个部门联合进行护航、护渔演习.
背景材料:近年来由于世界各国大力发展海洋经济、加强海洋能力开发,海洋争端也呈上升趋势.为增强海洋执法能力、维护海洋领土,近期我国多个部门联合进行护航、护渔演习.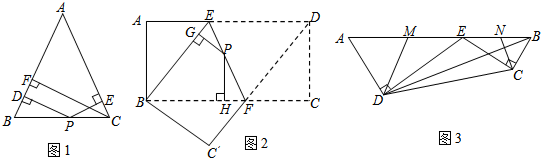
 如图,在△ABC中,已知AB=AC,∠A=45°,BD⊥AC于点D.根据该图可以求出tan22.5°=$\sqrt{2}$-1.
如图,在△ABC中,已知AB=AC,∠A=45°,BD⊥AC于点D.根据该图可以求出tan22.5°=$\sqrt{2}$-1.