题目内容
16.已知抛物线y=ax2+bx+c过(-2,3),(4,3)两点,那么抛物线的对称轴为直线x=1.分析 根据二次函数的图象具有对称性,由抛物线y=ax2+bx+c过(-2,3),(4,3)两点,可以得到它的对称轴,本题得以解决.
解答 解:∵抛物线y=ax2+bx+c过(-2,3),(4,3)两点,
∴抛物线的对称轴为直线x=$\frac{-2+4}{2}=1$,
故答案为:x=1.
点评 本题考查二次函数的性质,解题的关键是明确二次函数的性质,知道二次函数的图象具有对称性.

练习册系列答案
相关题目
6.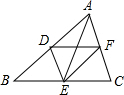 如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
 如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )| A. | AB⊥AC | B. | AB=AC | C. | AB=BC | D. | AC=BC |
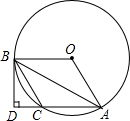 如图,AB是⊙O的弦,点O关于AB的对称点C在⊙O上,过点B作BD⊥AC交AC的延长线于点D.
如图,AB是⊙O的弦,点O关于AB的对称点C在⊙O上,过点B作BD⊥AC交AC的延长线于点D.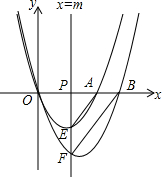 如图,动直线x=m(m>0)分别交x轴,抛物线y=x2-3x和y=x2-4x于点P,E,F,设点A,B为抛物线y=x2-3x,y=x2-4x与x轴的一个交点,连结AE,BF.
如图,动直线x=m(m>0)分别交x轴,抛物线y=x2-3x和y=x2-4x于点P,E,F,设点A,B为抛物线y=x2-3x,y=x2-4x与x轴的一个交点,连结AE,BF.
 如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上.
如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于A、B两个不同的点,其中点A在x轴上.