题目内容
6.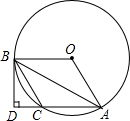 如图,AB是⊙O的弦,点O关于AB的对称点C在⊙O上,过点B作BD⊥AC交AC的延长线于点D.
如图,AB是⊙O的弦,点O关于AB的对称点C在⊙O上,过点B作BD⊥AC交AC的延长线于点D.(1)求证:BD是⊙O的切线;
(2)若⊙O的半径为2,请直接写出BD的长.
分析 (1)欲证明BD是⊙O的切线,只要证明∠OBD=90°,先四边形AOBC是菱形,得OB∥AD,根据两直线平行同旁内角互补即可解决问题.
(2)连接OC,先证明△OBC,△OAC都是等边三角形,在RT△BCD中利用30度性质即可解决问题.
解答 (1)证明:∵点O关于AB的对称点C在⊙O上,
∴AO=AC,BO=BC,
∵AO=OB,
∴AO=OB=BC=CA,
∴四边形AOBC是菱形,
∴AD∥OB,
∴∠D+∠OBD=180°,
∵BD⊥AD,
∴∠D=90°,
∴∠OBD=90°,
∴BD⊥OB,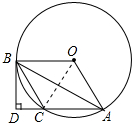
∵OB是⊙O的半径,
∴DB是⊙O的切线.
(2)连接OC,由(1)可知四边形AOBC是菱形,
∴OB=OC=BC=OA=AC,
∴△OBC,△OAC都是等边三角形,
∴∠BCO=∠ACO=60°,
∴∠ACB=120°,
∴∠BCD=180°-∠ACB=60°,
在RT△BCD中,∵∠D=90°,BC=2,∠DBC=30°,
∴CD=$\frac{1}{2}$BC=1,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$.
点评 本题考查切线的判定、菱形的判定、等边三角形的判定等知识,解题的关键是灵活运用圆的有关知识,掌握切线的判定方法,属于中考常考题型.

练习册系列答案
相关题目
15.-5的绝对值是( )
| A. | 5 | B. | -$\frac{1}{5}$ | C. | -5 | D. | $\frac{1}{5}$ |
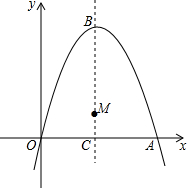 如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为点A,顶点为点B.抛物线的对称轴与x轴交于点C,点M在抛物线的对称轴上,且纵坐标为1.
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为点A,顶点为点B.抛物线的对称轴与x轴交于点C,点M在抛物线的对称轴上,且纵坐标为1. 如图所示的图案绕点O顺时针旋转,至少旋转120°后,与原来的图案重合.
如图所示的图案绕点O顺时针旋转,至少旋转120°后,与原来的图案重合. 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$. 如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.
如图,AE∥BF,AC、BD分别是∠BAD、∠ABC的平分线,且AC交BF于点C,BD交AE于点D,连接CD.求证:四边形ABCD是菱形.