题目内容
6.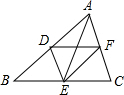 如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )| A. | AB⊥AC | B. | AB=AC | C. | AB=BC | D. | AC=BC |
分析 根据等腰三角形性质和三角形的中位线求出AE⊥DF,根据三角形的中位线求出DE∥AC,EF∥AB,得出四边形ADEF是平行四边形,再根据菱形的判定推出即可.
解答 解:AB=AC,
理由是:∵AB=AC,E为BC的中点,
∴AE⊥BC,
∵D、F分别为AB和AC的中点,
∴DF∥BC,
∴AE⊥DF,
∵D、E、F分别是△ABC的边AB、BC、AC的中点,
∴EF∥AD,DE∥AF,
∴四边形ADEF是平行四边形,
∵AE⊥DF,
∴四边形ADEF是菱形,
即只有选项B的条件能推出四边形ADEF是菱形,选项A、C、D的条件都不能推出四边形ADEF是菱形,
故选B.
点评 本题考查了等腰三角形的性质,三角形的中位线,平行四边形的判定,菱形的判定的应用,能得出四边形ADEF是平行四边形是解此题的关键.

练习册系列答案
相关题目
18.据国家统计局公告,2015年我国国内生产总值达到67.7亿元,将数67700000000000用科学记数法表示应为( )
| A. | 6.77×1012 | B. | 67.7×1012 | C. | 6.77×1013 | D. | 67.7×1013 |
15.有四个式子:①$\sqrt{18}=3\sqrt{2}$;②$\sqrt{9}=±3$;③${(\sqrt{5}+1)^2}=6$;④3a3•2a2=6a6,从这四个式子中随机抽取一个,抽到的式子不正确的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
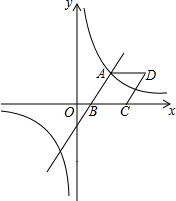 如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B.
如图,已知一次函数y=$\frac{3}{2}$x-3与反比例函数y=$\frac{k}{x}$的图象相交于点A(4,n),与x轴相交于点B. 如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D,抛物线y=$\frac{1}{4}$x2+bx+c经过B、C、D三点.
如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D,抛物线y=$\frac{1}{4}$x2+bx+c经过B、C、D三点.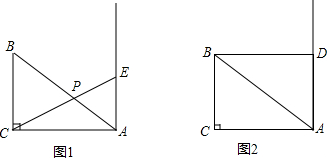 如图,△ABC中,∠ACB=90°,BC=6,AC=8.点E与点B在AC的同侧,且AE⊥AC.
如图,△ABC中,∠ACB=90°,BC=6,AC=8.点E与点B在AC的同侧,且AE⊥AC. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,有下列四个结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=$\sqrt{2}$;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论是①②④.(填写序号即可)
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,有下列四个结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=$\sqrt{2}$;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论是①②④.(填写序号即可)