题目内容
7.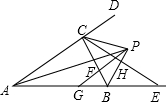 如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:
如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:①GA=GP;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④FP=FC,
其中正确的判断有(填序号)①②③④.
分析 ①根据角平分线的性质和平行线的性质即可得到结论;
②根据角平分线的性质和三角形的面积公式即可求出结论;
③根据线段垂直平分线的性质即可得结果;
④根据角平分线的性质和平行线的性质即可得到结果.
解答 解:①∵AP平分∠BAC,
∴∠CAP=∠BAP,
∵PG∥AD,
∴∠APG=∠CAP,
∴∠APG=∠BAP,
∴GA=GP;
②∵AP平分∠BAC,
∴P到AC,AB的距离相等,
∴S△PAC:S△PAB=AC:AB,
③∵BE=BC,BP平分∠CBE,
∴BP垂直平分CE(三线合一),
④∵∠BAC与∠CBE的平分线相交于点P,可得点P也位于∠BCD的平分线上,
∴∠DCP=∠BCP,
又∵PG∥AD,
∴∠FPC=∠DCP,
∴FP=FC,
故①②③④都正确.
故答案为:①②③④.
点评 本题主要考查了角平分线的性质和定义,平行线的性质,等腰三角形的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
18.下列函数关系式中,一定是反比例函数的是( )
| A. | y=$\frac{6}{x}$ | B. | y=-$\frac{12}{x}$+1 | C. | y=$\frac{k}{x}$ | D. | y=-$\frac{5}{2x}$-1 |
2.在下列说法中,正确的是( )
| A. | 如果两个三角形全等,则它们必是关于直线成轴对称的图形 | |
| B. | 如果两个三角形关于某直线成轴对称,那么它们是全等三角形 | |
| C. | 等腰三角形底边中线是对称轴 | |
| D. | 一条线段是关于经过该线段中点的直线成轴对称的图形 |
19.已知$\frac{x}{2}=\frac{y}{3}=\frac{z}{5}$,则$\frac{x+3y-z}{2x-y+z}$的值是( )
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{2}$ |
 如图,已知AB⊥BC,AD⊥CD.求证:∠A+∠C=180°.
如图,已知AB⊥BC,AD⊥CD.求证:∠A+∠C=180°.