题目内容
17.(1)为了探究三角形内角和,把∠B和∠A剪下后拼在一起,请你用量角器量一量,∠BCD=180°,所以∠A+∠B+∠ACB=180°.(2)如图,延长BC至D,过点C作CE′∥AB
∵CE∥AB
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠A(两直线平行,内错角相等)
∵∠1+∠2+∠ACB=180°(平角定义)
∴∠A+∠B+∠ACB=180°(等量代换)
归纳:三角形内角和等于180°.
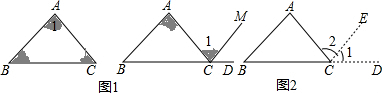
分析 (1)根据拼接法证明三角形内角和定理即可;
(2)利用平行线的性质来证明三角形的内角和是180°即可.
解答 解:(1)为了探究三角形内角和,把∠B和∠A剪下后拼在一起,用量角器量一量,∠BCD=180°,所以∠A+∠B+∠ACB=180°;
(2)如图,延长BC至D,过点C作CE′∥AB
∵CE∥AB
∴∠1=∠B(两直线平行,同位角相等)
∠2=∠A(两直线平行,内错角相等)
∵∠1+∠2+∠ACB=180°(平角定义)
∴∠A+∠B+∠ACB=180°(等量代换)
归纳:三角形内角和等于180°,
故答案为:180;180;B;两直线平行,同位角相等;A两直线平行,内错角相等;180;180;180.
点评 此题考查三角形内角和定理,关键是根据三角形内角和定理的两种证明方法进行解答.

练习册系列答案
相关题目
 如图,已知点A(m,n)、点B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,∠OAB=90°,AO=AB,求$\frac{m}{n}$的值.
如图,已知点A(m,n)、点B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,∠OAB=90°,AO=AB,求$\frac{m}{n}$的值.
 如图所示是某工厂的大门,它是由一个正方形和一个半圆组成的,正方形的边长为5米,一辆装货的卡车宽为4米,高为6米,则这辆卡车能否通过此大门?说明理由.
如图所示是某工厂的大门,它是由一个正方形和一个半圆组成的,正方形的边长为5米,一辆装货的卡车宽为4米,高为6米,则这辆卡车能否通过此大门?说明理由.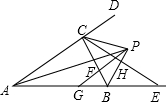 如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论:
如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,下列结论: