题目内容
4.化简:(1)$\frac{2}{b}$$\sqrt{{ab}^{3}}$•(-$\frac{3}{2}$$\sqrt{{a}^{3}b}$)÷3$\sqrt{\frac{b}{a}}$(a>0,b>0)
(2)$\frac{2}{3}$x$\sqrt{9x}$+6x$\sqrt{\frac{y}{x}}$+y$\sqrt{\frac{x}{y}}$-x2$\sqrt{\frac{1}{x}}$.
分析 (1)先对原式化简,然后再约分即可解答本题;
(2)先对原式化简,再合并同类项即可解答本题.
解答 解:(1)$\frac{2}{b}$$\sqrt{{ab}^{3}}$•(-$\frac{3}{2}$$\sqrt{{a}^{3}b}$)÷3$\sqrt{\frac{b}{a}}$(a>0,b>0)
=-$\frac{2b}{b}\sqrt{ab}×\frac{3a}{2}\sqrt{ab}×\frac{\sqrt{a}}{3\sqrt{b}}$
=${a}^{2}\sqrt{ab}$;
(2)$\frac{2}{3}$x$\sqrt{9x}$+6x$\sqrt{\frac{y}{x}}$+y$\sqrt{\frac{x}{y}}$-x2$\sqrt{\frac{1}{x}}$
=$\frac{2}{3}x×3\sqrt{x}+6x×\frac{\sqrt{xy}}{x}+\sqrt{xy}-x\sqrt{x}$
=$2x\sqrt{x}+6\sqrt{xy}+\sqrt{xy}-x\sqrt{x}$
=$x\sqrt{x}+7\sqrt{xy}$.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式混合运算的计算方法.

练习册系列答案
相关题目
12.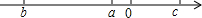 已知实数a、b、c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$+$\sqrt{(a-c)^{2}}$+$\sqrt{(b+c)^{2}}$的结果是( )
已知实数a、b、c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$+$\sqrt{(a-c)^{2}}$+$\sqrt{(b+c)^{2}}$的结果是( )
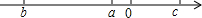 已知实数a、b、c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$+$\sqrt{(a-c)^{2}}$+$\sqrt{(b+c)^{2}}$的结果是( )
已知实数a、b、c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{(a-b)^{2}}$+$\sqrt{(a-c)^{2}}$+$\sqrt{(b+c)^{2}}$的结果是( )| A. | -3a | B. | a+2b | C. | 2b | D. | a |
19.已知n是正整数,且$\sqrt{45n}$也是一个正整数,则正整数n的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
9.下列调查中,适合采用全面调查的是( )
| A. | 对全国中学生心理健康现状的调查 | B. | 对某种食品合格情况的调查 | ||
| C. | 对某电视节目收视率的调查 | D. | 对你所在班级同学身高情况的调查 |
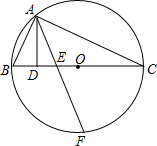 如图,△ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,连接OA,
如图,△ABC内接于⊙O,且BC是⊙O的直径,AD⊥BC于D,F是弧BC中点,且AF交BC于E,连接OA,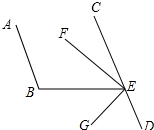 如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.
如图,已知AB∥CD,∠B=96°,EF平分∠BEC,EG⊥EF,求∠BEG和∠DEG的度数.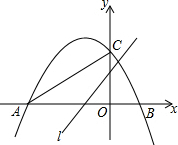 如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=$\sqrt{3}$x+m从点C开始沿y轴向下平移.
如图,抛物线y=ax2+bx+c(a≠0)的图象经过点A,B,C,已知点A的坐标为(-3,0),点B的坐标为(1,0),点C在y轴的正半轴上,且∠CAB=30°,若直线l:y=$\sqrt{3}$x+m从点C开始沿y轴向下平移.