��Ŀ����
������y����3x2��x��4��������Ľ��������( )
A. 3 B. 2 C. 1 D. 0
 A
����������������������߽���ʽy=��3x2��x+4����x=0����ã�y=4������������y��Ľ���Ϊ��0��4����
��y=0���õ���3x2��x+4=0����3x2+x��4=0���ֽ���ʽ�ã���3x+4����x��1��=0��
��ã�x1=����x2=1������������x��Ľ���ֱ�Ϊ������0������1��0����
���ϣ���������������Ľ������Ϊ3����ѡ��A��
A
����������������������߽���ʽy=��3x2��x+4����x=0����ã�y=4������������y��Ľ���Ϊ��0��4����
��y=0���õ���3x2��x+4=0����3x2+x��4=0���ֽ���ʽ�ã���3x+4����x��1��=0��
��ã�x1=����x2=1������������x��Ľ���ֱ�Ϊ������0������1��0����
���ϣ���������������Ľ������Ϊ3����ѡ��A��
 Сѧ�̲�ȫ��ϵ�д�
Сѧ�̲�ȫ��ϵ�д���ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
 B
���������������ĶԳƵĶ������֪��Bѡ������ĶԳ�ͼ��.��ѡB.
B
���������������ĶԳƵĶ������֪��Bѡ������ĶԳ�ͼ��.��ѡB. ����ABC�������������ӡ���3�����������������ɵ����������ɡ�ABC��������
A. ����ƽ��3����λ�õ��� B. ����ƽ��3����λ�õ���
C. ����ƽ��3����λ�õ��� D. ����ƽ��3����λ�õ���
 B
����������������
��ABC�������������ӡ���3�������ABC����ƽ��3����λ����ѡB��
B
����������������
��ABC�������������ӡ���3�������ABC����ƽ��3����λ����ѡB�� ��֪������y= -x2+mx+��7-2m����mΪ��������
��1��֤��������mΪ��ֵ����������x�����������ͬ�Ľ��㣻
��2������������x��Ľ���A��x1��0����B��x2��0���ľ���ΪAB=4��A��B����ߣ����������߽�y�����������C���������ߵĽ���ʽ��
 ��1��֤������������2�������ߵĽ���ʽΪy= -x2+2x+3��
�������������������1��Ҫ֤����������x�����������ͬ�Ľ���֤�������ߵ��б�ʽ������������֤���б�ʽ���������ɽ�����⣻
��2��������AB=4���Ե�|x2-x1|=4������x2-x1��2=��x2-x1��2-4x1x2=16��Ȼ�����ø���ϵ���Ĺ�ϵ���ɵõ�����m���̣��ⷽ�̼������m��Ҳ������������ߵĽ���ʽ��
����...
��1��֤������������2�������ߵĽ���ʽΪy= -x2+2x+3��
�������������������1��Ҫ֤����������x�����������ͬ�Ľ���֤�������ߵ��б�ʽ������������֤���б�ʽ���������ɽ�����⣻
��2��������AB=4���Ե�|x2-x1|=4������x2-x1��2=��x2-x1��2-4x1x2=16��Ȼ�����ø���ϵ���Ĺ�ϵ���ɵõ�����m���̣��ⷽ�̼������m��Ҳ������������ߵĽ���ʽ��
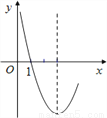
����... ��ͼ�����κ���y=x2-6x+n�IJ���ͼ����ͼ��ʾ��������x��һԪ���η���x2-6x+n=0��һ����Ϊx1=1������һ����x2= ___________.
 5��
��������������������ݶ��κ�����ͼ����x��Ľ�����ڶԳ���Գƣ�ֱ�����x2��ֵ��
�����������ͼ��֪���Գ���Ϊx=-
���ݶ��κ�����ͼ��ĶԳ��ԣ�
��ã�x2=5��
5��
��������������������ݶ��κ�����ͼ����x��Ľ�����ڶԳ���Գƣ�ֱ�����x2��ֵ��
�����������ͼ��֪���Գ���Ϊx=-
���ݶ��κ�����ͼ��ĶԳ��ԣ�
��ã�x2=5�� ��֪���κ���y=x2+bx-2��ͼ����x���һ������Ϊ��1��0����������x�����һ�����������ǣ�������
A. ��1��0�� B. ��2��0�� C. ��-2��0�� D. ��-1��0��
 C
�������������������x��1��y��0����y��x2��bx��2�ã�
0��1��b��2��
��b��1��
��Գ���Ϊx������
��x������
��x2����2��
����x�����һ�����������ǣ���2��0����
��ѡC��
C
�������������������x��1��y��0����y��x2��bx��2�ã�
0��1��b��2��
��b��1��
��Գ���Ϊx������
��x������
��x2����2��
����x�����һ�����������ǣ���2��0����
��ѡC�� ��ͼ����֪���κ���y��ax2��bx��c�IJ���ͼ����ͼ���֪����x��һԪ���η���ax2��bx��c��0���������ֱ���x1��1.6��x2��( )
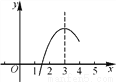
A. ��1.6 B. 3.2 C. 4.4 D. ���϶�����
 C
������������ͼ��֪�������ߵĶԳ���Ϊx=3����������������Գ�ͼ�����֪�����������x2��
��������
��������ͼ���֪��Գ���Ϊx=3��
������������Գ�ͼ��
����������x��������������x=3�Գƣ�
������x��һԪ���η���ax2+bx+c=0���������ֱ���x1��x2��
��������2��3=x1+x2��
��x1=1.6��
��x2=4.4��
...
C
������������ͼ��֪�������ߵĶԳ���Ϊx=3����������������Գ�ͼ�����֪�����������x2��
��������
��������ͼ���֪��Գ���Ϊx=3��
������������Գ�ͼ��
����������x��������������x=3�Գƣ�
������x��һԪ���η���ax2+bx+c=0���������ֱ���x1��x2��
��������2��3=x1+x2��
��x1=1.6��
��x2=4.4��
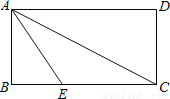
... ��ͼ��������ABCD�У�AB=2����E��BC�ϲ���AE=EC����������ֽƬ��AE�۵���ʹ��Bǡ������AC�ϣ���AC�ij�Ϊ���٣�
 4
����������������������۵������ʼ��ȱ߶ԵȽǵ����ʣ��ɵõ���BAE=��EAC=��ECA�������������ڽǺͶ���������á�ECA�Ķ������ٸ���ֱ�������ε����ʲ������AC�ij���
�����������ͼ�����B����AC�Ϻ�Ϊ��F.
���С�AFE�ա�ABE��
���AFE =��B =90�� ��AF =AB =2��
��FE��AC��
��AE=EC��
��CF =AF =2��...
4
����������������������۵������ʼ��ȱ߶ԵȽǵ����ʣ��ɵõ���BAE=��EAC=��ECA�������������ڽǺͶ���������á�ECA�Ķ������ٸ���ֱ�������ε����ʲ������AC�ij���
�����������ͼ�����B����AC�Ϻ�Ϊ��F.
���С�AFE�ա�ABE��
���AFE =��B =90�� ��AF =AB =2��
��FE��AC��
��AE=EC��
��CF =AF =2��... ij�����Ԯ��̽���ij����������·���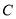 ������������,��֪����һ���������̽���A��B���3��,̽���������ļнǷֱ���
������������,��֪����һ���������̽���A��B���3��,̽���������ļнǷֱ���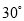 ��
��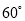 (��ͼ),��ȷ���������ڵ�C�����.(�����ȷ��
(��ͼ),��ȷ���������ڵ�C�����.(�����ȷ��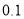 ��,�ο�����:
��,�����: 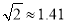 ,
,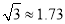 )
)
 �������ڵ�����ԼΪ��
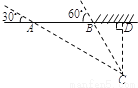
���������������������C��CD��AB�ڵ�D����������ó���CAD=30�㣬��CBD=60�㣬�ֱ����Rt��ACD��Rt��BCD�����Ǻ�����AD��BD�ú�CD�Ĵ���ʽ��ʾ��Ȼ�����AB=3�ó��𰸣�
��������������ڵ�
��̽���������ļн�Ϊ�ͣ� ��,��
��Rt��, �� �࣬
��Rt��, �� �࣬
�֡� �� ��ã�
���������ڵ�����...
�������ڵ�����ԼΪ��
���������������������C��CD��AB�ڵ�D����������ó���CAD=30�㣬��CBD=60�㣬�ֱ����Rt��ACD��Rt��BCD�����Ǻ�����AD��BD�ú�CD�Ĵ���ʽ��ʾ��Ȼ�����AB=3�ó��𰸣�
��������������ڵ�
��̽���������ļн�Ϊ�ͣ� ��,��
��Rt��, �� �࣬
��Rt��, �� �࣬
�֡� �� ��ã�
���������ڵ�����... 
