题目内容
9.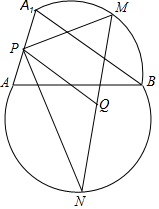 AB是圆的一条弦,它将圆分成两部分,M、N分别是两段弧的中点,以点B旋转中心将弓形AMB顺时针旋转一个角度成弓形A1MB、A1A的中点为P,MN的中点为Q.
AB是圆的一条弦,它将圆分成两部分,M、N分别是两段弧的中点,以点B旋转中心将弓形AMB顺时针旋转一个角度成弓形A1MB、A1A的中点为P,MN的中点为Q.求证:MN=2PQ.
分析 设弦AB是⊙O的弦,连接NO,由此NO交AB于D,交⊙O于C,连接CA、CB、CM、BM,只要证明△PNM∽△ANC,即可推出∠MPN=90°,由此即可解决问题.
解答 证明:设弦AB是⊙O的弦,连接NO,由此NO交AB于D,交⊙O于C,连接CA、CB、CM、BM.
∵$\widehat{AN}$=$\widehat{BN}$,
∴OD⊥AB,
∴AD=BD,$\widehat{AC}$=$\widehat{BC}$,
∵$\widehat{{A}_{1}M}$=$\widehat{BM}$=$\widehat{BC}$,
∴BC=BM,
∵弓形AMB顺时针旋转一个角度成弓形A1MB,
∴AB=BA1,∠ABA1=∠CBM,
∴△BCM∽△BAA1,
∴∠MCB=∠A1AB,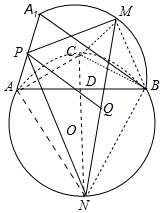 $\frac{CM}{A{A}_{1}}$=$\frac{BC}{BA}$,
$\frac{CM}{A{A}_{1}}$=$\frac{BC}{BA}$,
∵∠BAN=∠BCN,
∴∠PAN=∠MCN,
∵PA=PA1,
∴$\frac{CM}{A{A}_{1}}$=$\frac{CM}{2AP}$=$\frac{BC}{BA}$=$\frac{BC}{2BD}$,
∴$\frac{CM}{AP}$=$\frac{BC}{BD}$,
∵∠CDB=∠CAN=90°,∠CBD=∠ANC,
∴△DBC∽△ANC,
∴$\frac{BC}{BD}$=$\frac{NC}{NA}$,
∴$\frac{CM}{AP}$=$\frac{NC}{AN}$,
∴△APN∽△CMN,
∴$\frac{MN}{PN}$=$\frac{CN}{AN}$,∠CNM=∠PNA,
∴∠MNP=∠DNA,
∴△PNM∽△ANC,
∴∠NPM=∠NAC=90°,
∵MQ=QN,
∴PQ=QM=QN,
∴MN=2PQ.
点评 本题考查圆综合题、相似三角形的判定和性质、垂径定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,本题的难点多次证明相似三角形,熟练掌握两边成比例夹角相等两三角形相似这个判定定理,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | x2-(x-y+2z)=x2-x+y+2z | B. | 3x-[5x-(x-1)]=3x-5x-x+1 | ||
| C. | x-(-2x+3y-1)=x+2x-3y+1 | D. | (x-1)-(x2-2)=x-1-x2-2 |
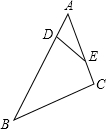 如图,在△ABC中,点D、E分别在AB、AC边上,且AD=2,AE=4,BD=10,CE=2,则DE:BC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,且AD=2,AE=4,BD=10,CE=2,则DE:BC等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 1:5 |
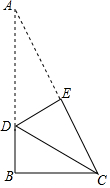 如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )
如图,折叠直角三角形ABC纸片,使两锐角顶点A、C重合,设折痕为DE.若AB=4,BC=3,则BD的值是( )| A. | $\frac{7}{8}$ | B. | 1 | C. | $\frac{9}{8}$ | D. | $\frac{2}{3}$ |
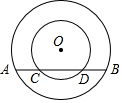 如图,两个同心圆,大圆半径为10cm,小圆的半径为6cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是16<AB≤20.
如图,两个同心圆,大圆半径为10cm,小圆的半径为6cm,若大圆的弦AB与小圆相交,则弦AB的取值范围是16<AB≤20.