题目内容
17.若a,b,c都是正数,满足$\frac{a}{bc}$+$\frac{b}{ca}$+$\frac{c}{ab}$≤$\frac{2}{a}$+$\frac{2}{b}$-$\frac{2}{c}$,则2c2-ac-bc-4c+2的最小值为-2.分析 由于a、b、c都是正数,根据不等式的性质,去掉分式的分母,整理不等式,根据完全平方公式和非负数的性质,得到a、b、c间关系,把a、b、c间关系代入代数式2c2-ac-bc-4c+2,变形成(c-m)2±n的形式,确定最小值.
解答 解:∵$\frac{a}{bc}$+$\frac{b}{ca}$+$\frac{c}{ab}$≤$\frac{2}{a}$+$\frac{2}{b}$-$\frac{2}{c}$,
∴$\frac{{a}^{2}}{abc}$+$\frac{{b}^{2}}{abc}$+$\frac{{c}^{2}}{abc}$≤$\frac{2bc}{abc}$+$\frac{2ac}{abc}$-$\frac{2ab}{abc}$,
∵a,b,c都是正数,
∴a2+b2+c2≤2bc+2ac-2ab,
即a2+b2+c2-2bc-2ac+2ab≤0
(a+b)2-2c(a+b)+c2≤0
∴(a+b-c)2≤0
∴a+b=c.
∵2c2-ac-bc-4c+2
=2c2-c(a+b)-4c+2
由于a+b=c,
∴2c2-c(a+b)-4c+2
=c2-4c+2
=(c-2)2-2
∵(c-2)2≥0
∴(c-2)2-2的最小值是-2.
点评 本题考查了完全平方公式、不等式的性质、非负数的性质、配方法及分式的化简求值.解决本题有两个关键:(1)根据完全平方公式和非负数的性质确定a、b、c间关系;(2)把要求最小值的代数式变形成(c-m)2±n的形式.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
6.若关于x的方程2m+x=1和方程3x-1=2x+1的解互为相反数,则m的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 0 | D. | -2 |
12.某地两种移动电话计费方式列表如表:
(1)一个月内,若通话时间分别为100分钟、200分钟或x分钟时,按两种计费方式各需
交费多少元?(请将未完成的答案填在表格内)
(2)当本地通话为x分钟时,请求出用全球通的话费与用神州行的话费的差.
(3)如果某个月通话时间为500分钟,用哪种计费方式更省钱?省多少元?
| 全球通 | 神州行 | |
| 月租费 | 30元/月 | 0 |
| 本地通话费 | 0.10元/分钟 | 0.30元/分钟 |
交费多少元?(请将未完成的答案填在表格内)
| 全球通(元) | 神州行(元) | |
| 100分 | 30+100×0.10=40元 | 100×0.30=30元 |
| 200分 | 30+200×0.10=50元 | 200×0.30=60元 |
| x分钟 | (30+0.1x)元 | 0.3x元 |
(3)如果某个月通话时间为500分钟,用哪种计费方式更省钱?省多少元?
6.关于x的一元二次方程(a-2)x2+x+a2-4=0的一个根是0,则a的值为( )
| A. | 2 | B. | -2 | C. | 2或-2 | D. | 一元二次方程 |
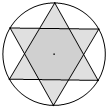 如图所示的“六芒星”图标是由圆的六等分点连接而成,若圆的半径为2$\sqrt{3}$,则图中阴影部分的面积为12$\sqrt{3}$.
如图所示的“六芒星”图标是由圆的六等分点连接而成,若圆的半径为2$\sqrt{3}$,则图中阴影部分的面积为12$\sqrt{3}$.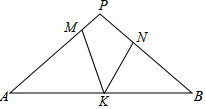 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为92°.
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为92°.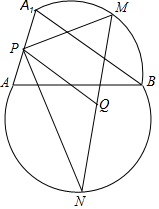 AB是圆的一条弦,它将圆分成两部分,M、N分别是两段弧的中点,以点B旋转中心将弓形AMB顺时针旋转一个角度成弓形A1MB、A1A的中点为P,MN的中点为Q.
AB是圆的一条弦,它将圆分成两部分,M、N分别是两段弧的中点,以点B旋转中心将弓形AMB顺时针旋转一个角度成弓形A1MB、A1A的中点为P,MN的中点为Q.