题目内容
11.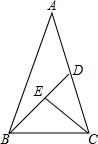 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )| A. | k2a | B. | k3a | C. | $\frac{a}{{k}^{2}}$ | D. | $\frac{a}{{k}^{3}}$ |
分析 由题意可知∠DCE=∠DBC=∠ECB=36°,∠CDE=∠CED=∠BCD=72°,推出BE=CE=CD,设DE=x,BC=BD=a,推出△DCE∽△DBC,可得$\frac{DC}{DB}$=$\frac{DE}{DC}$,推出$\frac{a-x}{a}$=$\frac{x}{a-x}$,即x2+ax-a2=0,可得x=$\frac{3a-\sqrt{5}a}{2}$或$\frac{3a+\sqrt{5}a}{2}$(舍弃),即DE=$\frac{3-\sqrt{5}}{2}$a,由此即可解决问题.
解答 解:由题意可知 ∠DCE=∠DBC=∠ECB=36°,∠CDE=∠CED=∠BCD=72°
∠DCE=∠DBC=∠ECB=36°,∠CDE=∠CED=∠BCD=72°
∴BE=CE=CD,设DE=x,BC=BD=a,
∴△DCE∽△DBC,
∴$\frac{DC}{DB}$=$\frac{DE}{DC}$,
∴$\frac{a-x}{a}$=$\frac{x}{a-x}$,
∴x2+ax-a2=0,
∴x=$\frac{3a-\sqrt{5}a}{2}$或$\frac{3a+\sqrt{5}a}{2}$(舍弃),
∴DE=$\frac{3-\sqrt{5}}{2}$a,
∵k=$\frac{\sqrt{5}+1}{2}$,
∴$\frac{1}{{k}^{2}}$=$\frac{3-\sqrt{5}}{2}$,
∴DE=$\frac{a}{{k}^{2}}$,
故选C.
点评 本题考查黄金分割、等腰三角形的性质和判定、相似三角形的判定和性质等知识,解题的关键是学会利用参数构建一元二次方程解决问题,属于中考选择题中的压轴题.

练习册系列答案
相关题目
 如图,已知△ABC中,∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是多少?
如图,已知△ABC中,∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是多少?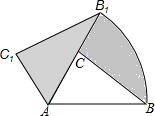 如图,在△ABC中,∠BAC=50°,AC=2,AB=3.现将△ABC绕A点逆时旋转50°得到△AB1C1,则图中的阴影部分的面积为$\frac{5}{4}$π.
如图,在△ABC中,∠BAC=50°,AC=2,AB=3.现将△ABC绕A点逆时旋转50°得到△AB1C1,则图中的阴影部分的面积为$\frac{5}{4}$π.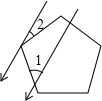 如图,一束平行太阳光照射到正五边形上,若∠1=44°,则∠2=28°.
如图,一束平行太阳光照射到正五边形上,若∠1=44°,则∠2=28°.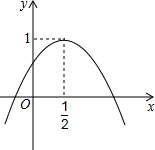 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc>0;②a=b;③a=4c-4;④方程ax2+bx+c=1有两个相等的实数根,其中正确的结论是③④.(只填序号即可).
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc>0;②a=b;③a=4c-4;④方程ax2+bx+c=1有两个相等的实数根,其中正确的结论是③④.(只填序号即可).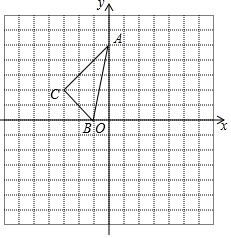 在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.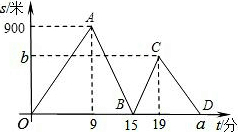 张强、刘明两位同学从实验中学出发到某中学参加作文比赛,张强不行行走一段时间后,刘明骑自行车沿同一条路线追赶,两人都是匀速前进,他们相距的路程s(单位:m)与张强出发的时间t(单位:min)之间的函数关系如图所示.
张强、刘明两位同学从实验中学出发到某中学参加作文比赛,张强不行行走一段时间后,刘明骑自行车沿同一条路线追赶,两人都是匀速前进,他们相距的路程s(单位:m)与张强出发的时间t(单位:min)之间的函数关系如图所示.