题目内容
20.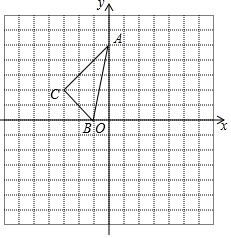 在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
在正方形网格中,每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.(1)作出将△ABC向右平移 2个单位长度后得到的△A1B1C1;
(2)作出将△ABC绕点O顺时针旋转90°后得到的△A2B2C2;
(3)求在(2)的旋转变换中,线段BC扫过区域的面积(结果保留π)
分析 (1)利用网格特点和平移的性质画出点A、B、C的对应点A1、B1、C1,从而得到△A1B1C1;
(2)利用网格特点和旋转的性质画出点A1、B1、C1的对应点A2、B2、C2,从而得到△A2B2C2;
(3)根据扇形的面积公式,利用线段BC扫过区域的面积=S扇形COC2-S扇形BOB2进行计算即可.
解答 解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作;
(3)线段BC扫过区域的面积=S扇形COC2-S扇形BOB2=$\frac{90•π•(\sqrt{13})^{2}}{360}$-$\frac{90•π•{1}^{2}}{360}$=3π.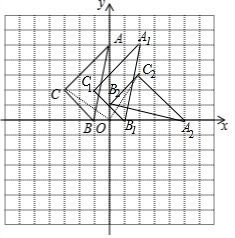
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知2a=3,2b=6,2c=12,则a,b,c的关系是( )
| A. | 2b<a+c | B. | 2b=a+c | C. | 2b>a+c | D. | a+b>c |
11.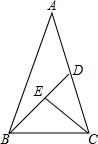 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )| A. | k2a | B. | k3a | C. | $\frac{a}{{k}^{2}}$ | D. | $\frac{a}{{k}^{3}}$ |
15.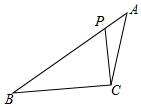 如图,已知△ABC,P为AB上一点,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知△ABC,P为AB上一点,以下条件中不能判定△ACP∽△ABC的是( )
 如图,已知△ABC,P为AB上一点,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知△ABC,P为AB上一点,以下条件中不能判定△ACP∽△ABC的是( )| A. | $\frac{AC}{AB}=\frac{CP}{BC}$ | B. | $\frac{AC}{AP}=\frac{AB}{AC}$ | C. | ∠APC=∠ACB | D. | ∠ACP=∠B |
9.在一次数学测验中,随机抽取了8份试卷,其得分如下表:
则这8名考生得分的中位数是86分.
| 得分 | 80 | 85 | 87 | 90 |
| 人数 | 1 | 3 | 2 | 2 |
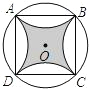 如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π.
如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π.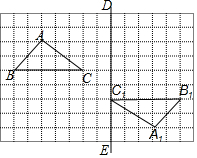 如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.
如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.