题目内容
16.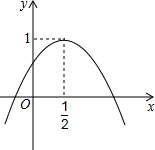 如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc>0;②a=b;③a=4c-4;④方程ax2+bx+c=1有两个相等的实数根,其中正确的结论是③④.(只填序号即可).
如图,二次函数y=ax2+bx+c的图象与y轴正半轴相交,其顶点坐标为($\frac{1}{2}$,1),下列结论:①abc>0;②a=b;③a=4c-4;④方程ax2+bx+c=1有两个相等的实数根,其中正确的结论是③④.(只填序号即可).
分析 ①根据抛物线的开口方向、对称轴位置和抛物线与y轴的交点坐标即可确定;
②根据抛物线的对称轴即可判定;
③根据抛物线的顶点坐标及b=-a即可判定;
④根据抛物线的最大值为1及二次函数与一元二次方程的关系即可判定.
解答 解:①∵根据图示知,抛物线开口方向向下,
∴a<0.
由对称轴在y轴的右侧知b>0,
∵抛物线与y轴正半轴相交,
∴c>0,
∴abc<0.故①错误;
②∵抛物线的对称轴直线x=-$\frac{b}{2a}$=$\frac{1}{2}$,
∴a=-b.
故②错误;
③∵该抛物线的顶点坐标为($\frac{1}{2}$,1),
∴1=$\frac{4ac-{b}^{2}}{4a}$,
∴b2-4ac=-4a.
∵b=-a,
∴a2-4ac=-4a,
∵a≠0,等式两边除以a,
得a-4c=-4,即a=4c-4.
故③正确;
④∵二次函数y=ax2+bx+c的最大值为1,即ax2+bx+c≤1,
∴方程ax2+bx+c=1有两个相等的实数根.
故④正确.
综上所述,正确的结论有③④.
故答案为:③④.
点评 本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c(a≠0)的系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
相关题目
7.“珍爱生命,拒绝毒品”,学校举行的2017年禁毒知识竞赛共有60道题,曾浩同学答对了x道题,答错了y道题(不答视为答错),且答对题数比答错题数的7倍还多4道,那么下面列出的方程组中正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=60}\\{x-7y=4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=60}\\{y-7x=4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=60-y}\\{x=7y-4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y=60-x}\\{y=7x-4}\end{array}\right.$ |
4.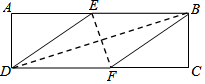 在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
②若DE2=BD•EF,则DF=2AD,则( )
 在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;
在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB,CD上),记它们的面积分别为S矩形ABCD和S菱形BEDF,若SABCD和SBFDE,给出如下结论:①若$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$,则tan∠EDF=$\frac{\sqrt{3}}{3}$;②若DE2=BD•EF,则DF=2AD,则( )
| A. | ①是假命题,②是假命题 | B. | ①是真命题,②是真命题 | ||
| C. | ①是假命题,②是真命题 | D. | ①是真命题,②是假命题 |
11.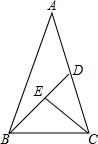 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )| A. | k2a | B. | k3a | C. | $\frac{a}{{k}^{2}}$ | D. | $\frac{a}{{k}^{3}}$ |
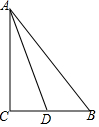 已知,如图,在△ABC中.∠C=90°,AD平分∠BAC.
已知,如图,在△ABC中.∠C=90°,AD平分∠BAC.
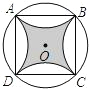 如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π.
如图是圆内接正方形ABCD,分别将$\widehat{AB}$,$\widehat{BC}$,$\widehat{CD}$,$\widehat{DA}$,沿边长AB,BC,CD,DA向内翻折,已知BD=2,则阴影部分的面积为4-4π. 如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADE交BC于点F.若BD⊥EF,请判断四边形EBFD是什么四边形,并说明理由.
如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADE交BC于点F.若BD⊥EF,请判断四边形EBFD是什么四边形,并说明理由.