题目内容
1.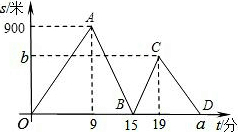 张强、刘明两位同学从实验中学出发到某中学参加作文比赛,张强不行行走一段时间后,刘明骑自行车沿同一条路线追赶,两人都是匀速前进,他们相距的路程s(单位:m)与张强出发的时间t(单位:min)之间的函数关系如图所示.
张强、刘明两位同学从实验中学出发到某中学参加作文比赛,张强不行行走一段时间后,刘明骑自行车沿同一条路线追赶,两人都是匀速前进,他们相距的路程s(单位:m)与张强出发的时间t(单位:min)之间的函数关系如图所示.(1)张强的速度是100m/min,请你解释点B所表示的意义:张强出发15min时被刘明追上;
(2)求刘明同学从实验中学到某中学的行驶速度;
(3)求实验中学与某中学的距离;
(4)求出图象中a,b的值;
(5)求线段CD所在直线的函数解析式,并写出自变量的取值范围.
分析 (1)根据函数图象可知,张强9分钟行驶900米,由此求得张强的速度,根据横轴与纵轴表示的意义以及点B的坐标即可解释点B所表示的意义;
(2)由图象可知,张强步行9分钟后刘明从实验中学出发,用6分钟追上张强,由此求出刘明与张强的速度差,进而得出刘明同学从实验中学到某中学的行驶速度;
(3)根据函数图象可知,刘明同学从实验中学到某中学所用的时间为10分钟,乘以速度即可得出实验中学与某中学的距离;
(4)用实验中学与某中学的距离除以张强的速度得出a的值,用实验中学与某中学的距离减去张强19分钟步行的路程得出b的值;
(5)根据点C和点D的坐标可以求得直线CD的解析式以及自变量的取值范围.
解答 解:(1)由题意可得,
张强的速度为:900÷9=100(m/min),
点B坐标(15,0)所表示的意义张强出发15min时被刘明追上.
故答案为:100,张强出发15min时被刘明追上;
(2)由题意和图象可得,
v刘明-v张强=$\frac{900}{15-9}$=150(m/min),
v刘明=100+150=250(m/min);
(3)由(2)知,v刘明=250m/min,
实验中学与某中学相距250×(19-9)=2500(m);
(4)a=2500÷100=25(min),
b=2500-100×19=600(m);
(5)设线段CD所在直线的函数解析式为s=kt+m.
∵C(19,600),D(25,0),
∴$\left\{\begin{array}{l}{19k+m=600}\\{25k+m=0}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-100}\\{m=2500}\end{array}\right.$,
即s=-100t+2500(19≤t≤25).
点评 本题考查一次函数的应用,路程、速度与时间关系的应用,读懂题目信息,准确识图,理清各时间段以及时间点两人的运动情况是解题的关键.

 学业测评一课一测系列答案
学业测评一课一测系列答案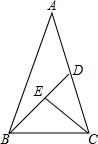 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )| A. | k2a | B. | k3a | C. | $\frac{a}{{k}^{2}}$ | D. | $\frac{a}{{k}^{3}}$ |
| 得分 | 80 | 85 | 87 | 90 |
| 人数 | 1 | 3 | 2 | 2 |
 如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADE交BC于点F.若BD⊥EF,请判断四边形EBFD是什么四边形,并说明理由.
如图,在平行四边形ABCD中,BE平分∠ABC交AD于点E,DF平分∠ADE交BC于点F.若BD⊥EF,请判断四边形EBFD是什么四边形,并说明理由.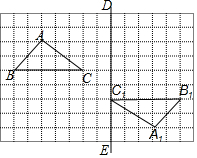 如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.
如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.