题目内容
6.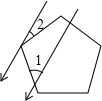 如图,一束平行太阳光照射到正五边形上,若∠1=44°,则∠2=28°.
如图,一束平行太阳光照射到正五边形上,若∠1=44°,则∠2=28°.
分析 先根据正五边形的性质求出∠3的度数,再由平行线的性质即可得出结论.
解答 解:∵图 中是正五边形.
中是正五边形.
∴∠3=108°.
∵太阳光线互相平行,∠1=44°,
∴∠2=180°-∠1-∠3=180°-44°-108°=28°.
故答案为:28°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同旁内角互补,解题的关键是:根据正五边形的性质求出∠3的度数.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
17.如果y=(1-m)x${\;}^{{m}^{2}-2}$是正比例函数,且y随x的增大而减小,则m的值为( )
| A. | m=-$\sqrt{3}$ | B. | m=$\sqrt{3}$ | C. | m=3 | D. | m=-3 |
17.某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).下表为装运甲、乙、丙三种水果的重量及利润.
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
| 甲 | 乙 | 丙 | |
| 每辆汽车能装的数量(吨)) | 4 | 2 | 3 |
| 每吨水果可获利润(千元) | 5 | 7 | 4 |
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
11.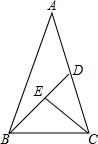 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
 如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )
如图,等腰△ABC中,底边BC=a,∠A=36°,∠ABC的平分线交AC于D,∠BCD的平分线交BD于E,设k=$\frac{\sqrt{5}+1}{2}$,则DE=( )| A. | k2a | B. | k3a | C. | $\frac{a}{{k}^{2}}$ | D. | $\frac{a}{{k}^{3}}$ |
15.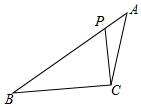 如图,已知△ABC,P为AB上一点,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知△ABC,P为AB上一点,以下条件中不能判定△ACP∽△ABC的是( )
 如图,已知△ABC,P为AB上一点,以下条件中不能判定△ACP∽△ABC的是( )
如图,已知△ABC,P为AB上一点,以下条件中不能判定△ACP∽△ABC的是( )| A. | $\frac{AC}{AB}=\frac{CP}{BC}$ | B. | $\frac{AC}{AP}=\frac{AB}{AC}$ | C. | ∠APC=∠ACB | D. | ∠ACP=∠B |

 如图,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点顺时针方向旋转180°后得到四边形A1B1C1D1.
如图,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点顺时针方向旋转180°后得到四边形A1B1C1D1.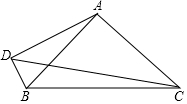 如图,己知∠CAB=90°,AB=$\frac{\sqrt{2}}{2}$BC,AD⊥BD,S△ABD=$\frac{3}{40}$BC2,sin∠CDB=$\frac{\sqrt{2}}{2}$.
如图,己知∠CAB=90°,AB=$\frac{\sqrt{2}}{2}$BC,AD⊥BD,S△ABD=$\frac{3}{40}$BC2,sin∠CDB=$\frac{\sqrt{2}}{2}$.