题目内容

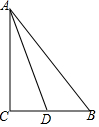
2．如图，已知△ABC中，∠C=90°，AD平分∠CAB，且BC=8，BD=5，则点D到AB的距离是多少？

分析 首先过点D作DE⊥AB于点E，由在△ABC中，∠C=90°，AD平分∠CAB，根据角平分线的性质，可得DE=CD，又由BC=8，BD=5，即可求得答案．

解答 解：过点D作DE⊥AB于点E，
∵在△ABC中，∠C=90°，AD平分∠CAB，
∴DE=CD，∵BC=8，BD=5，
∴CD=BC-BD=3，
∴DE=CD=3，
即点D到线段AB的距离是3．

点评 此题考查了角平分线的性质．此题比较简单，注意掌握辅助线的作法，注意数形结合思想的应用．

练习册系列答案
相关题目
13．已知二次函数y=mx2-3mx-4m（m≠0）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C且∠ACB=90°，则m的值为（　　）
A．±2B．±4C．±$\frac{1}{2}$D．±$\frac{1}{4}$
14．下列运算正确的是（　　）
A．a2•a3=a6B．2a2+a2=3a4C．a6÷a3=a2D．（ab2）3=a3b6
10．已知2a=3，2b=6，2c=12，则a，b，c的关系是（　　）
A．2b＜a+cB．2b=a+cC．2b＞a+cD．a+b＞c
17．某水果基地计划装运甲、乙、丙三种水果到外地销售（每辆汽车规定满载，并且只装一种水果）．下表为装运甲、乙、丙三种水果的重量及利润．
 甲乙丙
每辆汽车能装的数量（吨））423
每吨水果可获利润（千元）574
（1）用8辆汽车装运乙、丙两种水果共22吨到A地销售，问装运乙、丙两种水果的汽车各多少辆？
（2）水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售（每种水果不少于一车），假设装运甲水果的汽车为m辆，则装运乙、丙两种水果的汽车各多少辆？（结果用m表示）
（3）在（2）问的基础上，如何安排装运可使水果基地获得最大利润？最大利润是多少？
7．已知，如图，在△ABC中．∠C=90°，AD平分∠BAC．
（1）若BC=16，BD=10．求点D到AB的距离：
（2）若BC=8，BD：CD=5：3，AB=10，求△ABD的面积．
14．已知BM、CN分别是△A1BC的两个外角的角平分线，BA2、CA2分别是∠A1BC和∠A1CB的角平分线，如图①；BA3、CA3分别是∠A1BC和∠A1CB的三等分线（即∠A3BC=$\frac{1}{3}$∠A1BC，∠A3CB=$\frac{1}{3}$∠A1CB），如图②；依此画图，BAn、CAn分别是∠A1BC和∠A1CB的n等分线（即∠AnBC=$\frac{1}{n}$∠A1BC，∠AnCB=$\frac{1}{n}$∠A1CB），n≥2，且n为整数．
（1）若∠A1=70°，求∠A2的度数；
（2）设∠A1=α，请用α和n的代数式表示∠An的大小，并写出表示的过程；
（3）当n≥3时，请直接写出∠MBAn+∠NCAn与∠An的数量关系．
11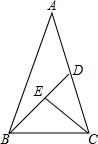．如图，等腰△ABC中，底边BC=a，∠A=36°，∠ABC的平分线交AC于D，∠BCD的平分线交BD于E，设k=$\frac{\sqrt{5}+1}{2}$，则DE=（　　）
A．k2aB．k3aC．$\frac{a}{{k}^{2}}$D．$\frac{a}{{k}^{3}}$
12．若ax+y=6，ay=3，则a2x=4．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网