题目内容
11.利用因式分解计算:(1)8×7582-2582×8;
(2)$\frac{5{2}^{2}-4{8}^{2}}{25{6}^{2}-24{4}^{2}}$.
分析 (1)先提取公因式8,再利用平方差公式进行计算;
(2)分子和分母分别利用平方差公式分解因式后,再计算比较简单.
解答 解:(1)8×7582-2582×8,
=8×(7582-2582),
=8×(758+258)(758-258),
=8×1016×500,
=406400;
(2)$\frac{5{2}^{2}-4{8}^{2}}{25{6}^{2}-24{4}^{2}}$,
=$\frac{(52-48)(52+48)}{(256-244)(256+244)}$,
=$\frac{4×100}{12×500}$,
=$\frac{1}{15}$.
点评 本题主要运用平方差公式对所给式子进行因式分解,再进行计算即可求出结果.

练习册系列答案
相关题目
1.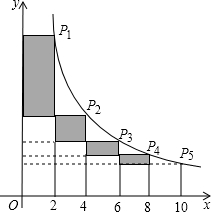 如图,在反比例函数y=$\frac{5}{x}$(x>0)的图象上有点P1、P2、P3、P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则S1+S2+S3+S4的值为( )
如图,在反比例函数y=$\frac{5}{x}$(x>0)的图象上有点P1、P2、P3、P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则S1+S2+S3+S4的值为( )
 如图,在反比例函数y=$\frac{5}{x}$(x>0)的图象上有点P1、P2、P3、P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则S1+S2+S3+S4的值为( )
如图,在反比例函数y=$\frac{5}{x}$(x>0)的图象上有点P1、P2、P3、P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则S1+S2+S3+S4的值为( )| A. | 4.5 | B. | 4.2 | C. | 4 | D. | 3.8 |
11.在△ABC中,AB=13,BC=10,BC边上的中线AD=12,则AC=( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
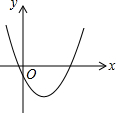 如图的抛物线是把抛物线y=$\frac{1}{2}$x2平移后经过(0,-1)和(4,-1)两点得到的.
如图的抛物线是把抛物线y=$\frac{1}{2}$x2平移后经过(0,-1)和(4,-1)两点得到的.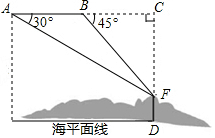 国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航,如图,在一次巡航过程中,巡航飞机飞行高度为2274米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1400米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度.(结果保留根号)
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航,如图,在一次巡航过程中,巡航飞机飞行高度为2274米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1400米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度.(结果保留根号) 如图,已知△ABC.
如图,已知△ABC.