题目内容
5.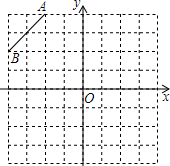 在所给的8×8的正方形网格中,按下列要求操作:(单位正方形边长为1)
在所给的8×8的正方形网格中,按下列要求操作:(单位正方形边长为1)(1)请在第二象限内的格点上找一点C,使△ABC是以AB为底的等腰三角形,且腰长为无理数,并写出C点的坐标(-1,1);
(2)在图中画出△ABC关于点O的中心对称三角形△A1B1C1,标出相应点字母.
分析 (1)要等腰,可见顶点要在底的垂直平分线上,要腰长为无理数,则腰长要是网格的对角线.依此找点就可,答案不唯一.
(2)将△ABC的各顶点绕点O旋转180°后,找到对应点,顺次连接得到的△A1B1C1.
解答 解:(1)如图所示:
腰AC的长=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴C点坐标为:(-1,1);
(2)所作图形如图所示.
故答案为:-1,1.
点评 本题考查了根据旋转变换作图,涉及到掌握网格的应用,及对无理数的理解,解答本题的关键是根据网格结构作出对应点的位置,然后顺次连接.

练习册系列答案
相关题目
15. 如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
 如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )| A. | ED=CD | B. | ∠DAC=∠B | C. | ∠C>2∠B | D. | BD=AD |
20.某商品经过连续两次降价后售价为256元,原售价289元.设平均每次降价的百分率为x,则下面所列方程中正确的是( )
| A. | 289(1-x)2=256 | B. | 256(1-x)2=289 | C. | 289(1-2x)=256 | D. | 256(1-2x)=289 |
10.在Rt△ABC中,∠C=90°,tanB=$\frac{5}{3}$,则cosA=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{3\sqrt{34}}{34}$ | D. | $\frac{5\sqrt{34}}{34}$ |
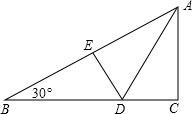 如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是8.
如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是8.