题目内容
13.解方程(1)x2-4x-1=0
(2)(3x+2)2=4(x-3)2.
分析 (1)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可;
(2)两边开方,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)x2-4x-1=0,
x2-4x=1,
x2-4x+4=1+4,
(x-2)2=5,
x-2=±$\sqrt{5}$,
x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$;
(2)(3x+2)2=4(x-3)2,
两边开方得:3x+2=±2(x-3),
解得:x1=-8,x2=$\frac{4}{5}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
1.在△ABC中,∠A:∠B:∠C=1:2:3,AB=a,则CB等于( )
| A. | $\frac{a}{2}$ | B. | $\frac{a}{3}$ | C. | $\frac{a}{4}$ | D. | 以上结果都不对 |
8.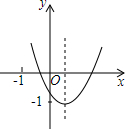 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
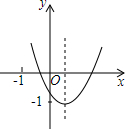 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )| A. | a<0 | B. | 2a+3b=0 | C. | a-b+c<0 | D. | c<-1 |
2.近似数1.40所表示的准确数a的范围是( )
| A. | 1.395≤a<1.405 | B. | 1.35≤a<1.45 | C. | 1.30<a<1.50 | D. | 1.400≤a<1.405 |
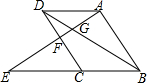 如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.
如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3. 如图为一次函数y=kx+b的图象,则一次函数y=bx+k的图象大致是( )
如图为一次函数y=kx+b的图象,则一次函数y=bx+k的图象大致是( )


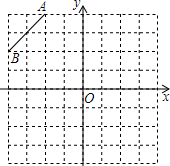 在所给的8×8的正方形网格中,按下列要求操作:(单位正方形边长为1)
在所给的8×8的正方形网格中,按下列要求操作:(单位正方形边长为1)