题目内容
14.阅读下面问题:$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1;$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}$-$\sqrt{2}$;$\frac{1}{\sqrt{5}+2}$=$\sqrt{5}$-2.
猜测:(1)$\frac{1}{\sqrt{7}+\sqrt{6}}$的值;
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$(n为正整数)的值.
(3)根据你的猜测计算:
$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+L+$\frac{1}{\sqrt{98}+\sqrt{99}}$+$\frac{1}{\sqrt{99}+\sqrt{100}}$的值.
分析 (1)根据观察,可发现规律:两个相邻自然数的算术平方根和的倒数等于这两个相邻自然数的算术平方根的差,可得答案;
(2)根据观察,可发现规律:两个相邻自然数的算术平方根和的倒数等于这两个相邻自然数的算术平方根的差,可得答案;
(3)根据规律:两个相邻自然数的算术平方根和的倒数等于这两个相邻自然数的算术平方根的差,可得答案.
解答 解:(1)原式=$\sqrt{7}$-$\sqrt{6}$;
(2)原式=$\sqrt{n+1}$-$\sqrt{n}$;
(3)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{99}$-$\sqrt{98}$+$\sqrt{100}$-$\sqrt{99}$
=10-1=9.
点评 本题考查了分母有理化,发现规律:两个相邻自然数的算术平方根和的倒数等于这两个相邻自然数的算术平方根的差是解题关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
2.近似数1.40所表示的准确数a的范围是( )
| A. | 1.395≤a<1.405 | B. | 1.35≤a<1.45 | C. | 1.30<a<1.50 | D. | 1.400≤a<1.405 |
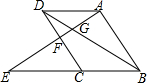 如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.
如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.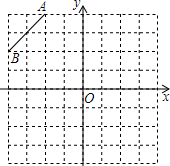 在所给的8×8的正方形网格中,按下列要求操作:(单位正方形边长为1)
在所给的8×8的正方形网格中,按下列要求操作:(单位正方形边长为1)
 已知:如图,△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.则∠F的度数35°;DH的长6.
已知:如图,△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.则∠F的度数35°;DH的长6.