题目内容
16.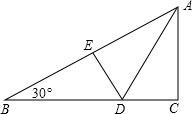 如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是8.
如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是8.
分析 由折叠的性质可知;DC=DE,∠DEA=∠C=90°,在Rt△BED中,∠B=30°,故此BD=2ED,从而得到BC=3BC,于是可求得DE=8.
解答 解:由折叠的性质可知;DC=DE,∠DEA=∠C=90°,
∵∠BED+∠DEA=180°,
∴∠BED=90°.
又∵∠B=30°,
∴BD=2DE.
∴BC=3ED=24.
∴DE=8.
故答案为:8.
点评 本题主要考查的是翻折的性质、含30°直角三角形的性质,根据题意得出BC=3DE是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
7.下列命题中,假命题是( )
| A. | 长度相等的弧是等弧 | |
| B. | 等弧必须是同圆或等圆中的弧,否则不能互相重合 | |
| C. | 度数相等的弧不一定是等弧 | |
| D. | 等弧的度数相等 |
1.在△ABC中,∠A:∠B:∠C=1:2:3,AB=a,则CB等于( )
| A. | $\frac{a}{2}$ | B. | $\frac{a}{3}$ | C. | $\frac{a}{4}$ | D. | 以上结果都不对 |
8.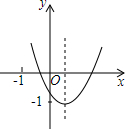 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
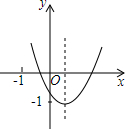 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线x=$\frac{1}{3}$,则下列结论中,正确的是( )| A. | a<0 | B. | 2a+3b=0 | C. | a-b+c<0 | D. | c<-1 |
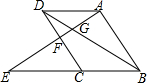 如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.
如图,?ABCD,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=2,GF=1,则EF=3.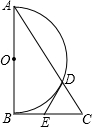 如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.
如图,在Rt△ABC中,∠ACB=90°,以AB为直径作半圆O交AC于点D,点E为BC的中点,连接DE.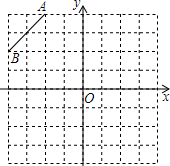 在所给的8×8的正方形网格中,按下列要求操作:(单位正方形边长为1)
在所给的8×8的正方形网格中,按下列要求操作:(单位正方形边长为1)